Monte Carlo方法

置信区间

假设一个随机变量$X$服从正态分布$X\sim N(\mu,\sigma^2)$, 那么通过正态分布表可知

如果$X_1,\cdots,X_n$是$n$个独立同分布且满足$X_i\sim N(\mu,\sigma^2)$的随机变量(即有$n$个独立同分布的样本), 定义随机变量

那么根据大数定律和中心极限定理可知, $Y\sim N\left(\mu,\dfrac{\sigma^2}{n}\right)$. 因此

把$\left[\mu-1.96\dfrac{\sigma}{\sqrt{n}},\mu+1.96\dfrac{\sigma}{\sqrt{n}}\right]$称为95%置信区间.

类似可得99%置信区间是$\left[\mu-2.57\dfrac{\sigma}{\sqrt{n}},\mu+2.57\dfrac{\sigma}{\sqrt{n}}\right]$.

但是一般情况下我们并不知道$\mu$和$\sigma$的值, 我们只能用$n$次观测到的$X_i$的取值来作估计, 计算出$X_i$的平均值来作为$\mu$的估计值$\hat{\mu}$, 并计算$X_i$的样本方差来作为$\sigma$的估计值$\hat{\sigma}$. 也就是说, 如果$X_i$的取值为$x_i$, 那么我们取

以及

$X_i$的具体取法.

假设我们要做$M$次成功概率为$p$的独立重复试验($p$是多少我们不知道), 观测到的成功次数为$m$, 那么我们估计成功概率是$\hat{p}=\dfrac{m}{M}$. 这样, $\hat{p}$是个随机变量, 满足$M\hat{p}\sim B(M,p)$.

所以在前一小节中, 我们就取$X_i$为$\hat{p}_i$, 即做$n$次“$M$次独立重复试验”, 相当于一共做$N=Mn$次独立重复试验, 但分成$n$批去做(得到$n$个样本), 把每次做完得到的概率估计值$\hat{p}_i$记录下来作为样本均值. 然后根据$\hat{p}_i(i=1,\cdots,n)$的值算出均值$\hat{\mu}$与方差$\hat{\sigma}$.

假设$\hat{p}_i$均服从正态分布$N\left(\hat{\mu},\hat{\sigma}^2\right)$, 那么根据上面的讨论可知, $95\%$置信区间的长度是$2\times 1.96\dfrac{\hat{\sigma}}{\sqrt{n}}.$ 类似地, 我们可以知道$99\%$置信区间的长度是$2\times 2.57\dfrac{\hat{\sigma}}{\sqrt{n}}.$

在写程序的时候, 如果总共做$N$次独立重复试验, 那么我们可以假设$n=100$(即抽100次样本), $M=\dfrac{N}{n}$(即每个样本都是做$M$次独立重复试验).

用Monte Carlo方法估计$\pi$的近似值

为了计算$\pi$的近似值, 我们可以采用Monte-Carlo方法: 随机在正方形区域$[0,1]\times[0,1]$中撒点, 计算出位于以圆心为原点、半径为1的四分之一圆的点的占比$\hat{p}$. 假如我们撒了$M$个点后, 有$m$个点位于四分之一圆中, 那么我们有$\hat{p}=\dfrac{m}{M}$.

写一个简单的函数实现用Monte-Carlo方法计算$\pi$的近似值, 要求返回$\pi$的近似值和置信区间中的标准差.

用Monte Carlo方法计算多重积分

我们用Monte-Carlo方法来计算$d$维球$B_d$的体积, 其中

这里$|x|_2=\sqrt{x_1^2+\cdots+x_d^2}$. 计算$B_d$可以通过如下的积分来得到:

其中,

(1)在Python或Matlab中, 写一个函数HyperballVolume(dim,N,n), 其中, 输入值dim是维数, N是点的个数, n表示分成$n$组做试验得到$n$个样本. 返回值为体积的估计值和$99\%$置信区间的长度.

(2)取$N=10^7$, $n=100$, 画出维数$1\le d\le 15$情形关于体积的折线图, 并显示$99\%$置信区间范围. 下图是取$N=10^6$情形的样例图.

(3)保持$N$不变, 改变$n$的值(例如取$n=1$, $n=10^3$, $n=10^5$, $n=10^7$等等), 看看对结果会产生什么影响?

(1)请不要使用$B_d$体积的精确表达式来计算置信区间.

(2)如果同学们会写并行算法, 那么在随机采样的步骤可以并行化处理, 速度会更快.

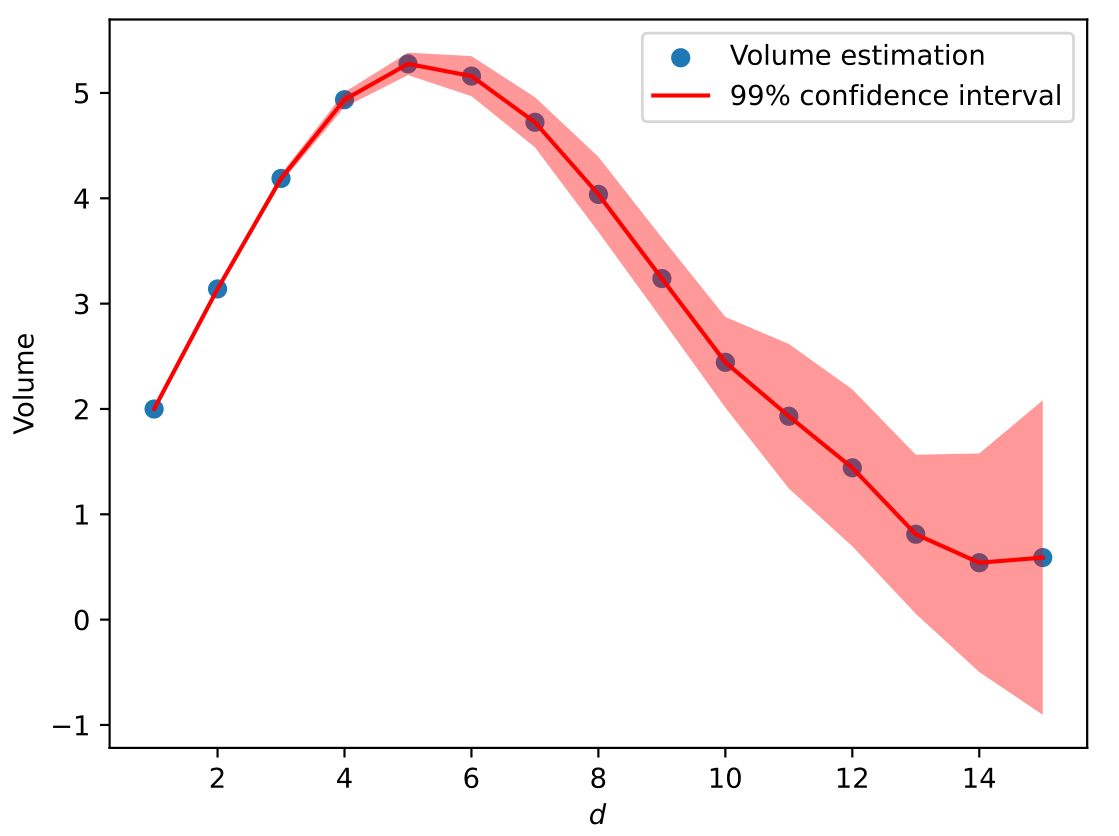
图1：体积$B_d$关于维数$d$在$1\le d\le 15$的折线图与$99\%$置信区间

附录：Python代码

import numpy as np
import random
import matplotlib.pyplot as plt

def hyperball_volume(dim, N, n = 100):
    point = np.zeros(dim)
    M = int(N / n)
    res = np.zeros(n) 

    for k in range(n):       #统计n次概率估计值, 后面计算均值和方差要用
        count = 0
        for i in range(M):   #每次统计，都要进行M次独立重复试验
            for j in range(dim):
                point[j]=random.random()*2-1
            dist = np.linalg.norm(point, ord=2)
            if(dist>1) :
                continue
            count+=1
    
        res[k] = count/M*pow(2,dim) #注意d维边长为2的正方体体积是2^d.

    #计算标准差和均值
    sigma = np.sqrt(np.var(res))
    vol = np.mean(res)

    return vol,sigma

if __name__ == "__main__":
    vol = np.zeros(15)
    sigma = np.zeros(15)
    con_lower = np.zeros(15) #置信区间的下界
    con_upper = np.zeros(15) #置信区间的上界
    N = 10000000 #N = 1000000, 100000 for testing
    n = 100
    for i in range(15):
        (vol[i],sigma[i]) = hyperball_volume(i+1, N, n)
        print(vol[i],sigma[i])
        con_lower[i] = vol[i] - 2.57*sigma[i]/np.sqrt(n)
        con_upper[i] = vol[i] + 2.57*sigma[i]/np.sqrt(n)
    
    # 画图
    plt.scatter(range(1,16), vol)
    plt.plot(range(1,16), vol, 'r')
    plt.fill_between(range(1,16),con_lower,con_upper, facecolor='red', alpha=0.4)
    plt.xlabel(r'$d$')
    plt.ylabel('Volume')
    plt.legend(["Volume estimation", r"99% confidence interval"], loc="upper right")
    plt.show()