参考文献:
[1] M. Raissi, P. Perdikaris, G.E. Karniadakis, Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, Journal of Computational Physics, Volume 378, 2019, 686-707, https://doi.org/10.1016/j.jcp.2018.10.045.
[2] C. Basdevant, M. Deville, P. Haldenwang, J. Lacroix, J. Ouazzani, R. Peyret, P. Orlandi, A. Patera, Spectral and finite difference solutions of the Burgers equation, Computers & fluids 14 (1986) 23-41.
修正Bessel函数
考虑下面的常微分方程(其中$\nu$是实数常量)
\[z^2\dfrac{\mathrm{d}^2y}{\mathrm{d}z^2}+z\dfrac{\mathrm{d}y}{\mathrm{d}z}-(z^2+\nu^2)y=0.\]它的解称为修正Bessel函数(modified Bessel function).
第一类修正Bessel函数构成修正Bessel方程的一组基本解, 它可通过如下定义:
\[I_{\nu}(z) = \left(\dfrac{z}{2}\right)^{\nu}\sum\limits_{k=0}^{\infty}\dfrac{(\frac{z^2}{4})^k}{k!\Gamma(\nu+k+1)}.\]第二类修正Bessel函数构成修正Bessel方程的独立于$I_{\nu}(z)$的另一组基本解, 它可通过如下定义:
\[K_{\nu}(z) = \dfrac{\pi}{2\sin(\pi \nu)}\cdot\left(I_{-\nu}(z)-I_{\nu}(z)\right).\]在Matlab中, 调用besseli可得到第一类修正Bessel函数, 调用besselk可得到第二类修正Bessel函数.
在Python中, 调用scipy.special.iv可得到第一类修正Bessel函数, 调用scipy.special.kv可得到第二类修正Bessel函数.
具体使用方法可参考Matlab自带的说明文档以及scipy包的说明文档.
Burgers方程
用深度学习来求解偏微分方程是当前的大热点, 比如内嵌物理信息的神经网络(Physics Informed Neural Networks, PINN)$^{[1]}$就是用了神经网络的工具, 把偏微分方程体现在损失函数, 然后用随机优化的方法(随机梯度下降法等等)来求解.
这篇论文里面涉及到求解Burgers方程:
\[\begin{aligned} &u_t+uu_x-\nu u_{xx}=0, \\ &u(0,x) = -\sin(\pi x) , \\ &u(t,-1) = u(t,1) = 0. \end{aligned}\]Burgers方程的解析解可以用Cole-Hopf变换得到, 它的解可写成级数形式$^{[2]}$
\[u(x,t) = 4\pi\nu\dfrac{\sum\limits_{n=1}^{\infty}na_ne^{-n^2\pi^2t\nu}\sin n\pi x } {a_0+2\sum\limits_{n=1}^{\infty}a_ne^{-n^2\pi^2t\nu}\cos n\pi x},\]其中, $a_n=(-1)^nI_n(\tfrac{1}{2\pi \nu})$, 这里$I_n(z)$表示第一类修正Bessel函数. 但是当$z\to \infty$时, $I_n(z)$和$e^z(2\pi z)^{-1/2}$是同阶的, 所以当$t$和$\nu$比较小的时候, 没办法用级数来算.
更好的办法是采用Cole-Hopf变换得到的积分计算:
\[u(t,x) = \dfrac{-\int_{-\infty}^{+\infty}\sin[\pi(x-\eta)]f(x-\eta)e^{-\frac{\eta^2}{4\nu t}}\mathrm{d}\eta} {\int_{-\infty}^{+\infty}f(x-\eta)e^{-\frac{\eta^2}{4\nu t}}\mathrm{d}\eta},\]其中, $f(y)=e^{-\frac{\cos (\pi y)}{2\pi\nu}}.$
我们用Hermite积分来计算它.
问题
考虑$\nu=\dfrac{0.01}{\pi}$.
1. 尝试用级数的方式, 通过截断有限项, 计算$u(t,x)$的近似解. 中间需要计算第一类修正Bessel函数(可调用现成的库函数), 你发现系数$a_n$有什么问题?
2.(选做) 复习Hermite正交多项式的定义, 我们想要用Hermite正交多项式$H_n(x)$构造出
\[\int_{-\infty}^{+\infty}g(x)e^{-x^2}\mathrm{d}x\]的数值积分公式. 能否给出用$H_n(x)$构造数值积分公式的误差估计?
3. 求出用$H_5(x)$构造出来的数值积分公式(权重系数可直接调用线性方程组求解的方法得出).
4. 补充下面的
burgers_real方法的“TODO”部分, 使得可以用它来求$u(t,x)$, 并画出彩色等高线图.
这里更推荐大家使用Python代码, 因为在深度学习中, 常用tensorflow或者pytorch包实现神经网络, 而它们也是通过Python语言调用的.
Matlab 代码
待补充.
Python 代码
import matplotlib.pyplot as plt
import numpy as np
# 可添加
def burgers_real(X, T, nu):
# 输入:
# X: 区间[-1,1]上的点构成的Nx维数组
# T: 区间[0,1]上的点构成的Nt维数组
# nu: Burgers方程中的参数ν
#
# 输出:
# U: 一个Nt * Nx维数组, U[j,i]表示在点(T[j],X[i])处Burgers方程的解.
Nx = len(X)
Nt = len(T)
U = np.zeros([Nt,Nx])
# TODO:请补充这部分代码.
return U
#调用方法并画图
nu = 0.01/pi
X, T = np.meshgrid(np.linspace(-1,1,201), np.linspace(0,1,101))
#提示:你可输出 X,T 发现 它们都是 101 行 201 列的数组. 所以定义 U 也必须是 101 行 201 列的数组.
U = burgers_real(X[0,:],T[:,0],nu)
lower_bound = np.min(U)
upper_bound = np.max(U)
print(lower_bound, upper_bound)
fig, ax = plt.subplots()
plt.title("Data")
levels = np.linspace(lower_bound,upper_bound,100) #对颜色渐进细致程度进行设置
cs = ax.contourf(T, X, U, levels,cmap=plt.get_cmap('Spectral'))
cbar = fig.colorbar(cs) #添加colorbar
plt.savefig('fig.eps') #保存图片为eps格式
plt.savefig('fig.png') #保存图片为png格式
输出图片示例
你输出的图片应该要长这样(下图是$\nu = \dfrac{0.2}{\pi}$的结果)
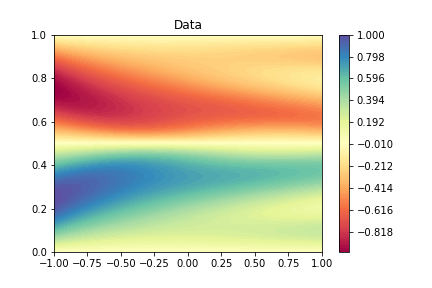
图:Burgers方程的解($\nu=\dfrac{0.2}{\pi}$)