用样条插值重构外旋轮线

用样条插值重构外旋轮线

问题描述

假如一个大圆的半径为$R$, 一个半径为$r$的小圆围绕着大圆滚动(如下图). 考虑离小圆圆心距离为$d$的一个附着在小圆上的点$P$, 于是$P$也会随着小圆的转动而转动.

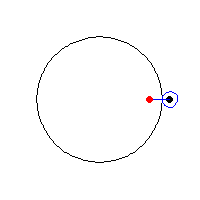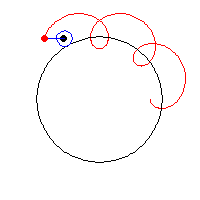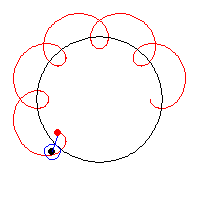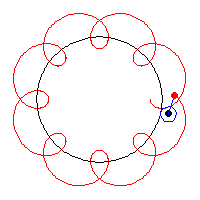
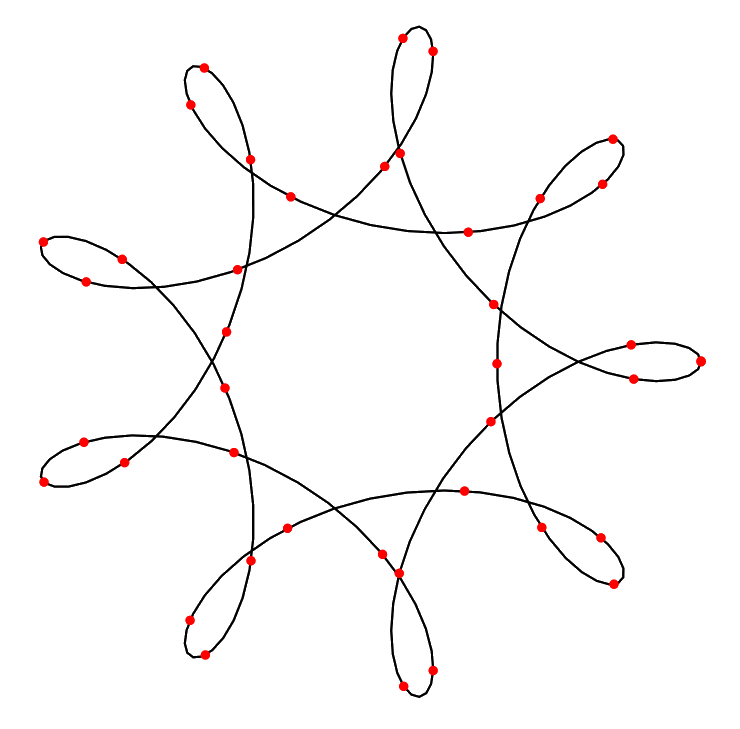
我们把$P$的运动轨迹称为外旋轮线(epitrochoid), 它的参数方程为

\[\begin{aligned} x(\theta)&=(R+r)\cos\theta+d\cos\left(\dfrac{R+r}{r}\theta\right), \\ y(\theta)&=(R+r)\sin\theta-d\sin\left(\dfrac{R+r}{r}\theta\right), \end{aligned}\]

在外旋轮线中取$R=5$, $r=2$, $d=3$, $\theta\in[0,4\pi]$. 它的图像如下.

用$n$个等距点(即$\theta_k=\tfrac{4\pi}{n}k$, $k=0,1,\cdots,n-1$, 如图为$n=40$的情形), 求函数$x(\theta)$和$y(\theta)$的三次样条插值函数$\tilde{x}(\theta)$和$\tilde{y}(\theta)$, 并画出参数曲线$\theta\mapsto(\tilde{x}(\theta),\tilde{y}(\theta))$的图像.

回顾：三次样条插值函数满足

\[S(x)=\left\{\begin{aligned} &S_1(x), &&x\in[x_1,x_2], \\ &\vdots \\ &S_i(x), &&x\in[x_i,x_{i+1}], \\ &\vdots \\ &S_n(x), &&x\in[x_n,x_{n+1}]. \end{aligned}\right.\] \[S_i(x)=\sum\limits_{k=1}^4A_{k,i}(x-x_i)^{k-1}, \qquad x\in[x_i,x_{i+1}],\]

其中系数为

\[\begin{aligned} A_{1,i}&=f_i, \\ A_{2,i}&=f[x_i,x_{i+1}]-\dfrac{h_i}{6}(m_{i+1}+2m_i), \\ A_{3,i}&=\dfrac{m_i}{2}, \\ A_{4,i}&=\dfrac{m_{i+1}-m_i}{6h_i}. \end{aligned}\]

所以需要求出$m_2,\cdots,m_{n+1}$即可得到三次样条插值函数.

由于这是等距结点, 所以$h_i=h=\dfrac{4\pi}{n}$. 再由于原来的问题可以看作周期三次样条插值问题, 根据$S(x)$函数值相等、导数相等和二次导数相等的条件, 可以写出线性方程组

\[\mathbf{Hm}=\dfrac{6}{h}\mathbf{d},\]

其中,

\[\begin{aligned} &\mathbf{H}=\begin{pmatrix} 4 & 1 & & & & 1 \\ 1 & 4 & 1 \\ & 1 & 4 & 1 \\ & & \ddots &\ddots & \ddots \\ & & & 1 & 4 & 1 \\ 1 & & & & 1 & 4 \end{pmatrix}, \\ &\mathbf{m}=(m_2,m_3,\cdots,m_{n+1})^T, \\ &\mathbf{d}=(d_2,d_3,\cdots,d_{n+1})^T, \end{aligned}\] \[\begin{aligned} &d_i=f[x_i,x_{i+1}]-f[x_{i-1},x_i], && i=2,\cdots,n, \\ &d_{n+1}=f[x_1,x_2]-f[x_n,x_{n+1}]. \end{aligned}\]

运行结果

最终运行结果如下, 可以发现当$n=160$时得到的样条插值函数图像与原来的函数图像非常接近.

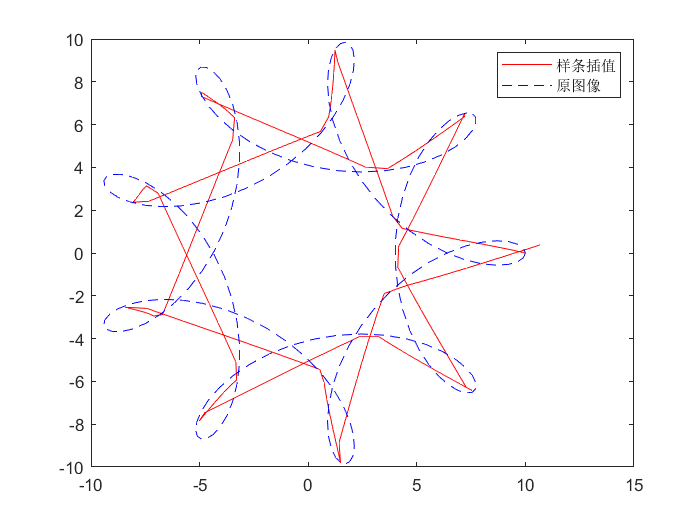
图1：原图像与$n=20$的样条插值图像

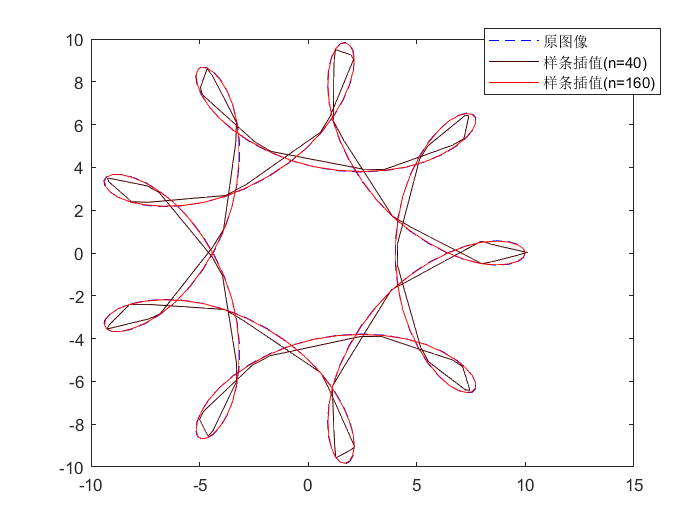
图2：原图像与$n=40$和$n=160$的样条插值图像

附录：Matlab代码

主程序

clf; %清空
f = @(x) (7*cos(x)+3*cos(3.5*x));
g = @(x) (7*sin(x)-3*sin(3.5*x));
xx = linspace(0,4*pi, 200);

ff_real = f(xx);
gg_real = g(xx);
plot(ff_real,gg_real, 'b--', 'DisplayName', '原图像');
hold on;

for n = [40,160] %可改变n的值
    h = 4*pi/n;
    
    xdata = linspace(0,4*pi,n+1);
    
    A1 = splineA(f, xdata);
    A2 = splineA(g, xdata);
    
    ff = spline(A1, xdata, xx);
    gg = spline(A2, xdata, xx);
    
    hold on;
    plot(ff,gg, 'Color', [n/160 0 0], 'DisplayName', '样条插值(n='+string(n)+')');
end
legend

样条函数的编写

function y = spline(A, xdata, x)
    %根据系数A和xdata复原的三次样条函数求x处的值
    m = length(xdata); %获取长度
    num = length(x);
    y = zeros(1,num);
    for k = 1:num
        for i = 1:m-1
            if (xdata(i)<= x(k) && x(k)<=xdata(i+1))
                %计算S_i(x)
                y(k) = A(4,i);
                for j = 1:3
                    y(k) = A(4-j, i) + (x(k)-xdata(i))*y(k);
                end
            end
        end
    end
end

function A = splineA(f, xdata)
    % 获取三次样条函数的系数A_{k,i}.
    n = length(xdata) - 1;
    h = xdata(2)-xdata(1);
    % 创建矩阵 H
    H = diag(4*ones(n,1),0)+diag(ones(n-1,1),1)+diag(ones(n-1,1),-1);
    H(1,n) = 1;
    H(n,1) = 1;
    
    % 创建向量 d
    d = zeros(n,1);
    for i = 1:n-1
        d(i) = (f(xdata(i+2))-f(xdata(i)))/h;
    end
    d(n) = ( f(xdata(2))-f(xdata(1)) - (f(xdata(n+1))-f(xdata(n))) )/h;
    H = sparse(H); %稀疏化
    m = H\d; %解方程组
    
    mtmp = m(n);
    m = [mtmp; m]; %变成n+1维向量
    
    %装配A_{1,i}
    A = zeros(4,n);
    for i = 1:n
        A(1,i) = f(xdata(i));
        A(2,i) = (f(xdata(i+1))-f(xdata(i)))/h-h/6*(m(i)+2*m(i+1));
        A(3,i) = m(i)/2;
        A(4,i) = (m(i+1)-m(i))/6/h;
    end
end