给定一些数据$\lbrace (x_i,y_i)\rbrace_{i=1}^m$, 其中$x_i\in\mathbb{R}^d$, $y_i\in\mathbb{R}$. 我们想用函数$y=f(x)$来拟合这些数据. 由于$(x_i,y_i)$不一定都在这条曲线上, 所以会有误差. 我们一般用均方误差(Mean-square Loss), 即
\[\mathcal{L}(f)=\dfrac{1}{m}\sum\limits_{i=1}^m|f(x_i)-y_i|^2\]来衡量误差. 我们把$\mathcal{L}$称为损失函数. 在求$f$的表达式的时候, 通过一定的优化方法让损失函数$\mathcal{L}$尽可能小, 即求解如下的优化问题, 使得可以得到一个近似的拟合函数:
\[\inf\limits_{f\in \mathcal{F}}\mathcal{L}(f),\]其中$\mathcal{F}$是由一族函数构成的集合.
线性最小二乘法
我们假设$x_i,y_i\in\mathbb{R}$. 考虑用直线$y=a+bx$来拟合这些数据.
当$m=2$时, 这就相当于插值, 此时误差为$0$. 但是当$m\ge 3$时, 一般情况下都会产生误差, 此时损失函数可以写作
\[\mathcal{L}(a,b):=\mathcal{L}(f)=\dfrac{1}{m}\sum\limits_{i=1}^m(ax_i+b-y_i)^2.\]根据极值存在的必要条件, 我们有
\[\left\{\begin{aligned} &\dfrac{\partial\mathcal{L}}{\partial a}=\dfrac{2}{m}\sum\limits_{i=1}^m x_i(ax_i+b-y_i)=0, \\ &\dfrac{\partial\mathcal{L}}{\partial b}=\dfrac{2}{m}\sum\limits_{i=1}^m(ax_i+b-y_i)=0. \end{aligned}\right.\]定义$\mathbb{R}^m$上的内积$(\boldsymbol{x},\boldsymbol{y})=\sum\limits_{i=1}^mx_iy_i,$ 并假设$\bar{x}=\dfrac{1}{m}\sum\limits_{i=1}^mx_i$, $\bar{y}=\dfrac{1}{m}\sum\limits_{i=1}^my_i$分别为$\lbrace x_i\rbrace$和$\lbrace y_i\rbrace$平均值, 那么上式可以化为
\[\begin{aligned} a(\boldsymbol{x},\boldsymbol{x})+bm\bar{x}&=(\boldsymbol{x},\boldsymbol{y}), \\ a\bar{x}+b&=\bar{y}. \end{aligned}\]上述方程组的解为
\[\left\{\begin{aligned} a&=\dfrac{(\boldsymbol{x},\boldsymbol{y})+m\bar{x}\bar{y}}{(\boldsymbol{x},\boldsymbol{x})-m\bar{x}\bar{x}} =\dfrac{\sum\limits_{i=1}^m (x_i-\bar{x})(y_i-\bar{y})}{\sum\limits_{i=1}^m (x_i-\bar{x})^2}, \\ b&=\bar{y}-a\bar{x}. \end{aligned}\right.\]这就是我们熟悉的一元线性回归模型(高中就学过了).
多项式拟合的最小二乘法
上述推导也可以推广为多项式的情形. 假如我们要用函数
\[f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\]来拟合$m$个数据$\lbrace (x_i,y_i)\rbrace$, 那么此时
\[\dfrac{\partial \mathcal{L}}{\partial a_k}=\dfrac{2}{m}\sum\limits_{i=1}^mx_i^k(a_0+a_1x_i+\cdots+a_nx_i^n-y_i)=0,\]其中, $i=0,1,\cdots,n.$ 沿用前面的内积的定义, 可以把上面的$n+1$条等式改写为如下的$n+1$阶的线性方程组:
\[\boldsymbol{Au}=\boldsymbol{b},\]其中, 对于向量$\boldsymbol{x}$, 记$\boldsymbol{x}^k=(x_1^k,x_2^k,\cdots,x_m^k)\in\mathbb{R}^m$, 并且
\[\boldsymbol{A}=\begin{pmatrix} (\boldsymbol{x}^n, \boldsymbol{x}^n) & (\boldsymbol{x}^n, \boldsymbol{x}^{n-1}) & \cdots & (\boldsymbol{x}^n,\boldsymbol{x}^0) \\ (\boldsymbol{x}^{n-1}, \boldsymbol{x}^n) & (\boldsymbol{x}^{n-1}, \boldsymbol{x}^{n-1}) & \cdots & (\boldsymbol{x}^{n-1},\boldsymbol{x}^0) \\ \vdots & \vdots & & \vdots \\ (\boldsymbol{x}^0, \boldsymbol{x}^n) & (\boldsymbol{x}^0, \boldsymbol{x}^{n-1}) & \cdots & (\boldsymbol{x}^0,\boldsymbol{x}^0) \end{pmatrix}\] \[\boldsymbol{u}=(a_n,a_{n-1},\cdots,a_0)^T, \quad \boldsymbol{b}=\begin{pmatrix} (\boldsymbol{x}^n, \boldsymbol{y}) \\ (\boldsymbol{x}^{n-1}, \boldsymbol{y}) \\ \vdots \\ (\boldsymbol{x}^0, \boldsymbol{y}) \end{pmatrix}.\]因此, 只需要求解上面的线性方程组即可得到多项式拟合函数.
一个算例
假如有以下数据:
\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline x & 0.000 & 0.895 & 1.641 & 2.512 & 3.542 & 4.054 & 4.602 & 5.063 & 5.354 & 5.617 \\ \hline y & 1.000 & 1.803 & 3.680 & 7.320 & 13.59 & 17.41 & 22.19 & 24.89 & 26.55 & 29.77 \\ \hline \end{array}\]用多项式函数拟合上面数据的Python代码如下:
import numpy as np
import matplotlib.pyplot as plt
def polyval(a, x): # 计算多项式 a[0]x^{n-1} + a[1]x^{n-2} + ... + a[n-1]
n = len(a)
m = len(x)
y = np.zeros(m)
for i in range(m): #计算多项式的算法
b = np.zeros(n)
b[0] = a[0]
for k in range(1,n):
b[k] = a[k] + b[k-1] * x[i]
y[i] = b[n-1]
return y
def polyfit(xdata, ydata, deg): #给定xdata和ydata, 返回多项式.
m = len(xdata)
n = deg + 1
xdatas = np.zeros([n,m])
xdatas[0] = np.ones(m)
for i in range(1,n): # 用不断迭代的方法得到xdata的幂次.
xdatas[i] = xdatas[i-1] * xdata
# 装配矩阵 A
A = np.zeros([n,n])
for i in range(n):
for j in range(n):
A[i][j] = np.dot(xdatas[n-1-i],xdatas[n-1-j])
# 装配右端向量 b
b = np.zeros(n)
for i in range(n):
b[i] = np.dot(xdatas[n-1-i],ydata)
# 解方程组
a = np.linalg.solve(A, b)
return a
if __name__ == "__main__":
m = 10
xdata = np.array([0.000, 0.895, 1.641, 2.512, 3.542, 4.054, 4.602, 5.063, 5.354, 5.617])
ydata = np.array([1.000, 1.803, 3.680, 7.320, 13.59, 17.41, 22.19, 24.89, 26.55, 29.77])
deg = 2
# 输出数据
a = polyfit(xdata, ydata, deg)
print(a)
yfit = polyval(a, xdata)
print('Loss:', np.linalg.norm(ydata-yfit)/m)
# 画图
x_draw = np.linspace(0, 6, 100)
y_draw = polyval(a, x_draw)
plt.plot(xdata,ydata, 'ro')
plt.plot(x_draw,y_draw, 'b')
plt.show()
对于二次函数拟合, 运行结果为:
\[a_2 = 0.7542712, \quad a_1 = 0.98752785 , \quad a_0 = 0.53554452.\]Loss: $0.17507558220264588$
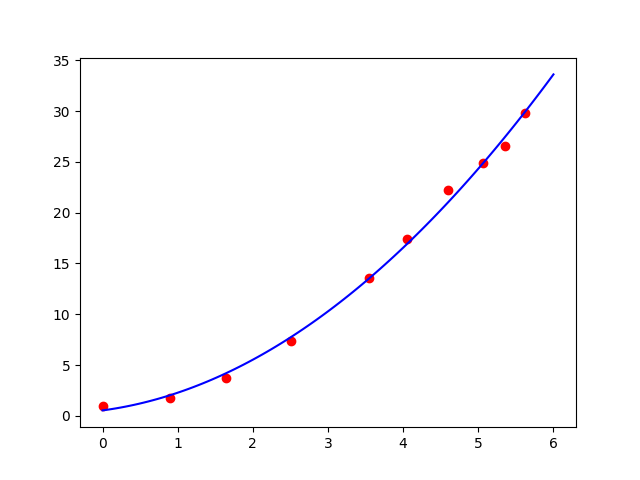
图1:用二次函数拟合给定数据
过拟合现象
假设$P^n$是不超过$n$次的多项式函数空间, 则
\[\inf\limits_{f\in P^{n+1}}\mathcal{L}(f) \le \inf\limits_{f\in P^{n}}\mathcal{L}(f).\]因此, 当拟合多项式的次数越高, 误差越小. 但是是否次数越高越好呢?
假如我用9次多项式来拟合上面的数据. 此时得到的结果如下图, 并且得到的Loss非常小, 为$0.00015833208434402744$.
可以发现, 虽然Loss比较小, 但是此时的拟合曲线也许并不是我们想要的, 而这就是过拟合(over-fitting)现象.

图2:用9次函数拟合给定数据
多项式拟合工具包(Matlab和Python)
事实上, 在Python的Numpy包以及Matlab中内置了多项式拟合的包, 我们可以直接调用它.
在Python中, 用polyfit作拟合的代码如下, 它的返回值是次数从大到小的拟合多项式的系数.
import numpy as np
import matplotlib.pyplot as plt
if __name__ == "__main__":
m = 10
xdata = np.array([0.000, 0.895, 1.641, 2.512, 3.542, 4.054, 4.602, 5.063, 5.354, 5.617])
ydata = np.array([1.000, 1.803, 3.680, 7.320, 13.59, 17.41, 22.19, 24.89, 26.55, 29.77])
deg = 2
a = np.polyfit(xdata,ydata,deg) #polyfit返回值是次数从大到小的拟合多项式的系数.
# 输出数据
print(a)
yfit = np.polyval(a, xdata) #这里np.polyval方法类似于我们之前写的polyval.
print('Loss:', np.linalg.norm(ydata-yfit)/m)
# 画图
x_draw = np.linspace(0, 6, 100)
xx_draw = x_draw * x_draw
y_draw = np.polyval(a, x_draw)
plt.plot(xdata,ydata, 'ro')
plt.plot(x_draw,y_draw, 'b')
plt.show()
运行结果:
\[a_2 = 0.7542712, \quad a_1 = 0.98752785 , \quad a_0 = 0.53554452.\]Loss: $0.17507558220264596$. 可以发现这跟我们前面手动写的输出结果几乎一模一样.
Matlab代码如下:
xdata = [0.000, 0.895, 1.641, 2.512, 3.542, 4.054, 4.602, 5.063, 5.354, 5.617];
ydata = [1.000, 1.803, 3.680, 7.320, 13.59, 17.41, 22.19, 24.89, 26.55, 29.77];
m = length(xdata);
deg = 2;
a = polyfit(xdata,ydata,deg) ;
% 输出数据
a
yfit = polyval(a, xdata);
fprintf("%.16f\n", norm(ydata-yfit)/m);
% 画图
x_draw = linspace(0, 6, 100);
y_draw = polyval(a, x_draw);
clf;
hold on;
plot(xdata,ydata, 'ro')
plot(x_draw,y_draw, 'b')
广义多项式拟合
事实上, 前面的多项式可以改为任意的函数, 即考虑用如下的函数作拟合:
\[y=f(x)=\sum\limits_{k=0}^{n}a_k\phi_k(x).\]其中, $\phi_k$是给定的函数, $\phi_0(x)=1$为常值函数. 仿照前面的推导可得如下线性方程组:
\[\boldsymbol{Au}=\boldsymbol{b},\]其中, 对于向量$\boldsymbol{x}$, 记$\phi^k=(\phi^k(x_1),\phi^k(x_2),\cdots,\phi^k(x_m))\in\mathbb{R}^m$, 并且
\[\boldsymbol{A}=\begin{pmatrix} (\phi^n, \phi^n) & (\phi^n, \phi^{n-1}) & \cdots & (\phi^n,\phi^0) \\ (\phi^{n-1}, \phi^n) & (\phi^{n-1}, \phi^{n-1}) & \cdots & (\phi^{n-1},\phi^0) \\ \vdots & \vdots & & \vdots \\ (\phi^0, \phi^n) & (\phi^0, \phi^{n-1}) & \cdots & (\phi^0,\phi^0) \end{pmatrix}\] \[\boldsymbol{u}=(a_n,a_{n-1},\cdots,a_0)^T, \quad \boldsymbol{b}=\begin{pmatrix} (\phi^n, \boldsymbol{y}) \\ (\phi^{n-1}, \boldsymbol{y}) \\ \vdots \\ (\phi^0, \boldsymbol{y}) \end{pmatrix}.\]把下面的代码的TODO部分改成可以用下面的广义多项式拟合:
\[f(x)=a_0+a_1f_1(x)+a_2f_2(x)+\cdots+a_nf_n(x).\]
def polyfit(xdata, ydata, f):
# 给定xdata和ydata, 返回(广义)多项式.
# f可以输入数字,如果输入数字,那么就表示多项式的次数.
# f也可以输入函数数组f=[f_1, ..., f_n],表示用常值函数和广义多项式拟合.
m = len(xdata)
if(type(f)==int): #多项式
n = f + 1 #f表示deg
xdatas = np.zeros([n,m])
xdatas[0] = np.ones(m)
for i in range(1,n): # 用不断迭代的方法得到xdata的幂次.
xdatas[i] = xdatas[i-1] * xdata
else: #函数数组
n = len(f) + 1 #f表示deg
xdatas = np.zeros([n,m])
xdatas[0] = np.ones(m)
# TODO: 请补充完整这里
# 装配矩阵 A
A = np.zeros([n,n])
for i in range(n):
for j in range(n):
A[i][j] = np.dot(xdatas[n-1-i],xdatas[n-1-j])
# 装配右端向量 b
b = np.zeros(n)
for i in range(n):
b[i] = np.dot(xdatas[n-1-i],ydata)
# 解方程组
a = np.linalg.solve(A, b)
return a
# 调用
if __name__ == "__main__":
m = 10
xdata = np.array([0.000, 0.895, 1.641, 2.512, 3.542, 4.054, 4.602, 5.063, 5.354, 5.617])
ydata = np.array([1.000, 1.803, 3.680, 7.320, 13.59, 17.41, 22.19, 24.89, 26.55, 29.77])
def f0(x):
return x
def f1(x):
return np.cos(x)
def f2(x):
return np.sin(x)
#二次多项式拟合
a1 = polyfit(xdata,ydata,2) #polyfit返回值是次数从大到小的拟合多项式的系数.
print(a1)
#用常值函数, x, cos(x), sin(x)拟合
f = [f0, f1, f2]
a2 = polyfit(xdata,ydata,f) #polyfit返回值是次数从大到小的拟合多项式的系数.
print(a2)