函数拟合：非线性数据拟合

线性化技巧
梯度下降法
用梯度下降法来优化损失函数
非线性拟合工具包
- Python
- Matlab
习题

给定一些数据$\lbrace (x_i,y_i)\rbrace_{i=1}^m$, 其中$x_i\in\mathbb{R}^d$, $y_i\in\mathbb{R}$. 我们想用函数$y=f(x)$来拟合这些数据. 由于$(x_i,y_i)$不一定都在这条曲线上, 所以会有误差. 我们一般用均方误差(Mean-square Loss), 即

\[\mathcal{L}(f)=\dfrac{1}{m}\sum\limits_{i=1}^m|f(x_i)-y_i|^2\]

来衡量误差. 我们把$\mathcal{L}$称为损失函数. 在求$f$的表达式的时候, 通过一定的优化方法让损失函数$\mathcal{L}$尽可能小, 即求解如下的优化问题, 使得可以得到一个近似的拟合函数：

\[\inf\limits_{f\in \mathcal{F}}\mathcal{L}(f),\]

其中$\mathcal{F}$是由一族函数构成的集合.

前面我们介绍了用广义多项式逼近和有理函数逼近. 今天我们探究用一般的非线性函数来作逼近的方法, 其中没有办法写成广义多项式或有理函数的形式. 例如, 用下面的函数来作逼近:

\[f(x)=\dfrac{a}{1+be^{cx}}\]

其中$a,b,c$都是未知的.

线性化技巧

如果一组数据$\lbrace (x_i,y_i)\rbrace_{i=1}^m$可以通过一个变换来线性化, 即存在函数$u,v$, 使得$\lbrace (u(x_i),v(y_i))\rbrace_{i=1}^m$可以用线性函数来逼近, 那么根据给定数据把函数$u,v$找出来即可.

假如有以下数据:
\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline x & -1.5 & -1 & -0.5 & 0 & 0.5 & 1 & 1.5 \\ \hline y & 0.04 & 0.17 & 0.65 & 1.39 & 1.85 & 1.90 & 1.99 \\ \hline \end{array}\]
用形如$y=\dfrac{2}{1+ae^{bx}}$的函数来逼近上面的数据.

首先我们需要作一定的变换来线性化:

\[y=\dfrac{2}{1+ae^{bx}} \Leftrightarrow \dfrac{2}{y}=1+ae^{bx} \Leftrightarrow \ln\left(\dfrac{2}{y}-1\right)=bx+\ln a.\]

因此, 取$u(x)=x$, $v(y)=\ln\left(\dfrac{2}{y}-1\right)$即可实现线性化. 我们用

\[\tilde{y}=bx+c, \qquad (\text{其中}c=\ln a)\]

来作拟合. Python代码如下:

import numpy as np
import matplotlib.pyplot as plt

if __name__ == "__main__": 
    xdata = np.array([-1.5, -1, -0.5, 0, 0.5, 1, 1.5])
    ydata = np.array([0.04, 0.17, 0.65, 1.39, 1.85, 1.90, 1.99])

    # 线性化处理
    yt = np.log(2.0/ydata-1.0) 
    u = np.polyfit(xdata,yt,1) #u[0]x+u[1]
    print(u)
    b = u[0]
    c = u[1]
    a = np.exp(c)

    # 画图
    xdraw = np.linspace(-1.5,1.5,100)
    ydraw = 2.0/(1+a*np.exp(b*xdraw))
    plt.plot(xdata,ydata, 'ro')
    plt.plot(xdraw,ydraw, 'b')
    plt.show()

Matlab代码如下:

xdata = [-1.5, -1, -0.5, 0, 0.5, 1, 1.5];
ydata = [0.04, 0.17, 0.65, 1.39, 1.85, 1.90, 1.99];

% 线性化处理
yt = log(2.0./ydata-1.0);
u = polyfit(xdata,yt,1)
b = u(1);
c = u(2);
a = exp(c);

% 画图
xplot = linspace(-1.5,1.5,100);
yplot = 2./(1+a*exp(b*xx));
clf;
plot(xplot,yplot,'b-');
hold on 
plot(xdata,ydata, 'ro');
legend('Curve', 'original', 'location', 'northwest');

运行结果：

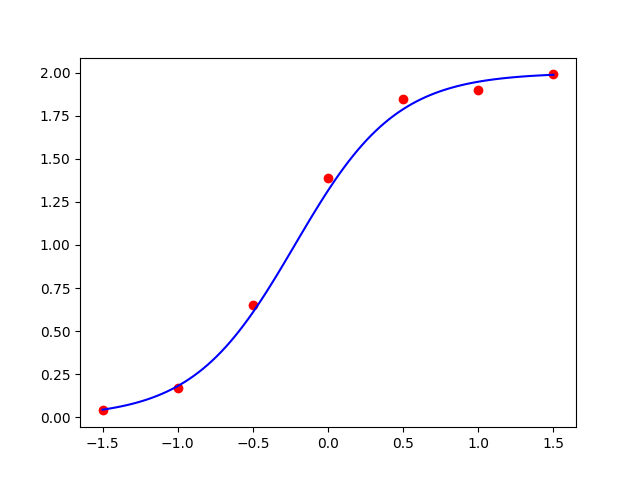
图1：用线性化技巧拟合给定数据

然而, 如果用线性化处理, 那么此时我们优化的损失函数并不是

\[\mathcal{L}(a,b)=\dfrac{1}{m}\sum\limits_{i=1}^m\left|\dfrac{2}{1+ae^{bx_i}}-y_i\right|^2\]

而是

\[\tilde{\mathcal{L}}(b,c)=\dfrac{1}{m}\sum\limits_{i=1}^m\left|bx_i+c-\ln\left(\dfrac{2}{y_i}-1\right)\right|^2.\]

优化$\tilde{\mathcal{L}}(b,c)$得到的最小值点$a=e^c$和$b$并不一定是$\mathcal{L}(a,b)$的最小值. 因此, 需要用其他方法来求$\mathcal{L}(a,b)$的最小值.

梯度下降法

关于梯度下降法的参考书: Luenberger, David \& Ye, Yinyu. (1984). Linear and Nonlinear Programming. doi:10.2307/1240727.

一般地, 设$J(\theta)$是$\mathbb{R}^n$中连续可微函数, 现在需要求它的最小值, 即求如下的优化问题:

\[\theta^{\ast} = \mathrm{arg}\min_{\theta} J (\theta)\]

把$J$的梯度记为

\[\nabla J=\left(\dfrac{\partial J}{\partial \theta_1},\cdots,\dfrac{\partial J}{\partial \theta_n}\right),\]

梯度下降法(gradient descent method)是下面的迭代算法:

\[\theta_{k+1}=\theta_k-\alpha_kg_k,\]

其中, $g_k=g(\theta_k)=\nabla J(\theta_k)^T$, 非负实数$\alpha_k$是步长(stepsize).

梯度下降法的计算过程就是沿梯度下降的方向迭代求解极小值, 换言之, 从$\theta_k$这一点开始, 我们沿着负梯度方向$-g_k$来进行搜索, 找到一点$\theta_{k+1}$, 使得$J(\theta_{k+1})\le J(\theta_k)$.

我们把步长设成常数, 迭代公式为

\[\theta_{k+1}=\theta_k-\eta\nabla J (\theta_k).\]

其中$\eta$在机器学习中也叫做学习率(learning rate). 终止准则可以取为$\vert\nabla J(\theta)\vert<\varepsilon$.

在梯度下降法的求解过程中, 只需求解损失函数的一阶导数, 计算代价相比二阶方法(需要用到Hessian矩阵的迭代算法)比较小, 可以在很多大规模数据集上应用.

但是，梯度下降法由于方向选择的问题, 得到的结果不一定是全局最优, 即参数寻优陷入了局部极小(local minima), 如图2所示. 这显然不是我们所希望的. 因此, 想办法把初值选为靠近全局最优点是关键.

除此之外, 梯度下降法每次迭代更新都需要遍历所有的数据, 当样本数据很多时, 计算量开销大, 计算速度慢.

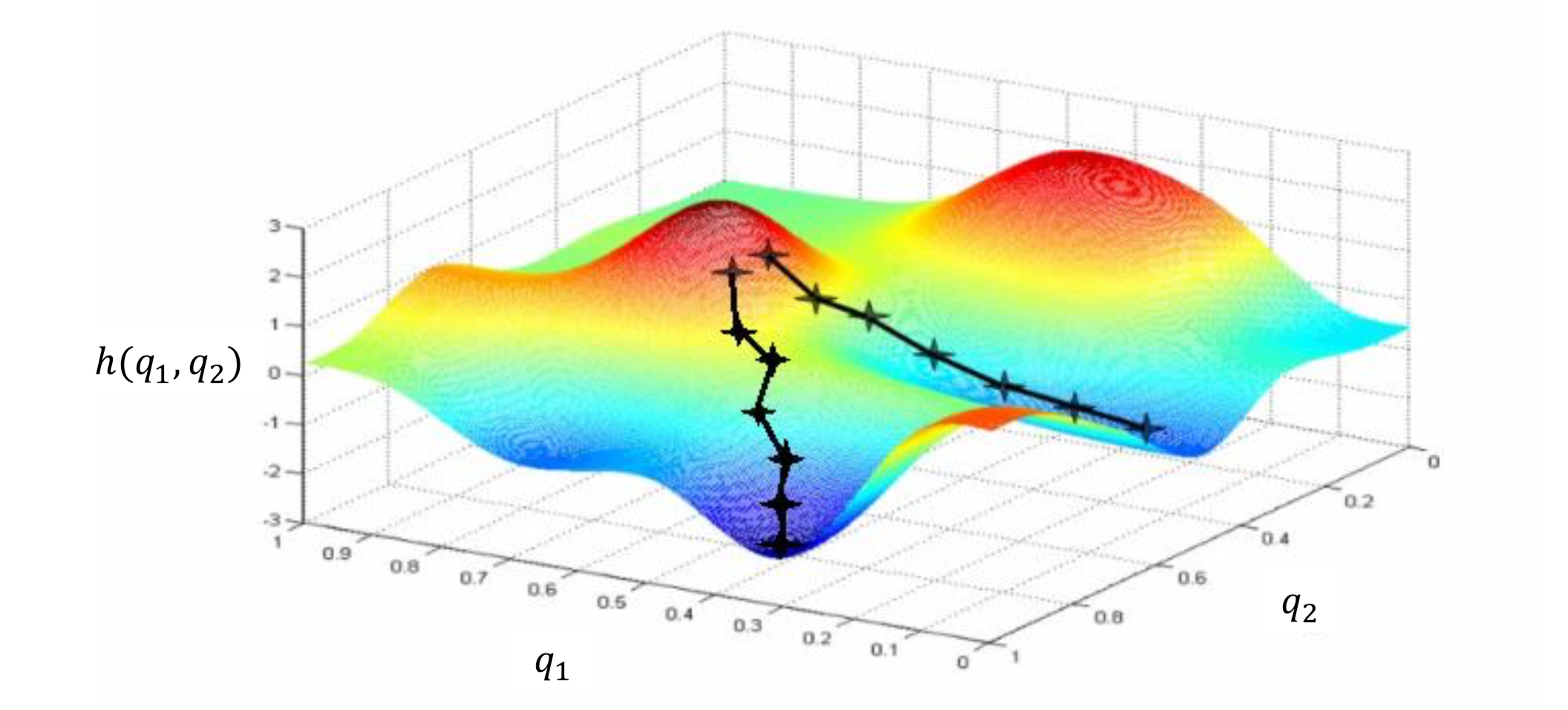
图2：梯度下降法陷入局部极小

一般来说学习率需要合理选取. 如果太低, 会导致收敛速度太慢; 如果太高, 会导致“跨过”了极小值点, 如图3.

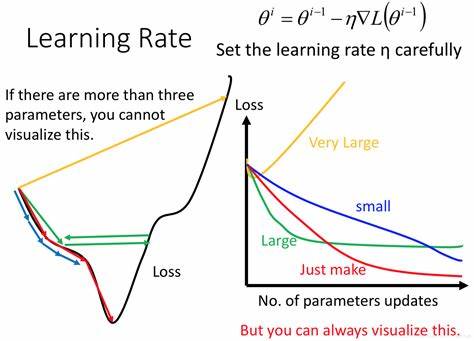
图3：学习率对收敛性的影响

用梯度下降法来优化损失函数

均方误差$\mathcal{L}(f)$的自变量是一些待定系数, 优化$\mathcal{L}(f)$可以用梯度下降法. 前面提到, 用线性化技巧并不能得到最优值, 但是我们可以猜测线性化技巧得到的结果非常接近最优值. 所以为了避免局部最优而得到全局最优, 一个合理的初值的选取方式是用线性化技巧得到的结果.

请在下面的代码基础上补全TODO部分, 完成梯度下降法优化函数optimize(f,df, x0, eps = 1e-8), 输入值分别为函数f、它的梯度df、初值x0、步长eta、终止准则的误差容限是eps(默认值为$10^{-8}$). 需要首先判断f, df, x0之间维数是否对应, 如果维数不对应就返回一个错误: Dimension does not match.
然后, 沿用前面的数据：
\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline x & -1.5 & -1 & -0.5 & 0 & 0.5 & 1 & 1.5 \\ \hline y & 0.04 & 0.17 & 0.65 & 1.39 & 1.85 & 1.90 & 1.99 \\ \hline \end{array}\]
用形如$y=\dfrac{2}{1+ae^{bx}}$的函数来逼近上面的数据. 先用线性化技巧得到了一个初值, 再用你写的梯度下降法来得到一个更好的值, 并画出图像.

import numpy as np
import matplotlib.pyplot as plt

def optimize(f,df,x0,eta,eps=1e-8):
    #输入: f(x1,...,xn), df=[df1,...,dfn], 其中dfi是f关于xi的偏导数. 
    #返回值: 迭代的最后一步x. 
    #先判断输入是否合理
    n = len(x0)
    assert f.__code__.co_argcount == n, 'Dimension of f does not match x0'
    assert len(df) == n, 'Dimension of df does not match x0'
    for i in range(n):
        assert df[i].__code__.co_argcount == n, 'Dimension of df does not match x0'
        
    #开始优化
    x = x0
    #TODO: 补全梯度下降法的代码.

    return x

if __name__ == "__main__": 
    #一个简单的算例来验证optimize
    def f(x1,x2):
        return x1*x1+x2*x2
    def df1(x1,x2):        #改成(x1,x2,x3)应该需要报错
        return 2*x1
    def df2(x1,x2):
        return 2*x2
    x0 = np.array([0.5,0.5])   #设置初始值
    x = optimize(f,[df1,df2],x0,eta)
    print(x)

非线性拟合工具包

Python

在Python中用非线性函数拟合数据的方法是scipy.optimize.curve_fit(). 具体使用方法可以参见这里

核心代码为

import scipy.optimize as opt

popt, pcov = opt.curve_fit(f,xdata,ydata,p0) 

用curve_fit()方法来对前面的线性化以后的结果作进一步优化的代码如下：

import numpy as np
import scipy.optimize as opt
import matplotlib.pyplot as plt

if __name__ == "__main__": 
    xdata = np.array([-1.5, -1, -0.5, 0, 0.5, 1, 1.5])
    ydata = np.array([0.04, 0.17, 0.65, 1.39, 1.85, 1.90, 1.99])

    # 变换
    yt = np.log(2.0/ydata-1.0) 
    u = np.polyfit(xdata,yt,1) #u[0]x+u[1]
    print(u)
    b = u[0]
    c = u[1]
    a = np.exp(c)

    #作curve_fit

    def f(x, a, b):
        y = 2.0/(1+a*np.exp(b*x))
        return y

    popt, pcov = opt.curve_fit(f,xdata,ydata,p0 = [a,b]) 

    #计算Loss
    err1 = np.linalg.norm(f(xdata,a,b) - ydata)/7
    err2 = np.linalg.norm(f(xdata,popt[0],popt[1]) - ydata)/7
    print(err1,err2)
    

输出值：popt为$[0.43798582 -3.13205546]$, err1为$0.016569358316672757$, err2为$0.009438304573712395$.

Matlab

在Matlab中, 用非线性函数拟合数据的方法是lsqcurvefit(). 具体使用方法可以在Matlab中输入```help lsqcurvefit``.

核心代码为

p = lsqcurvefit(@(x,xdata) 2./(1+x(1)*exp(x(2)*xdata)), p0, xdata, ydata);

用lsqcurvefit方法来对前面的线性化以后的结果作进一步优化的代码如下：

xdata = [-1.5, -1, -0.5, 0, 0.5, 1, 1.5];
ydata = [0.04, 0.17, 0.65, 1.39, 1.85, 1.90, 1.99];

% 线性化处理
yt = log(2.0./ydata-1.0);
u = polyfit(xdata,yt,1)
b = u(1);
c = u(2);
a = exp(c);

%% lsqcurvefit

p0 = [a b];
p = lsqcurvefit(@(x,xdata) 2./(1+x(1)*exp(x(2)*xdata)), p0, xdata, ydata);

y1 = 2./(1+a*exp(b*xdata));
y2 = 2./(1+p(1)*exp(p(2)*xdata));
err1 = norm(y1-ydata)/7.;
err2 = norm(y2-ydata)/7.;

输出值：$p = [0.4380, -3.1320]$. err1为$0.016569358316673$, err2为$0.009438304592826$.

习题

给定$x_i,y_i(i=0,1,\cdots,10)$作为拟合点和拟合点函数值,
\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline x & -1 & -0.8 & -0.6 & -0.4 & -0.2 & 0 & 0.2 & 0.4 & 0.6 & 0.8 & 1 \\ \hline y & -0.8669 & -0.2997 & 0.3430 & 1.0072 & 1.6416 & 2.2022 & 2.6558 & 2.9823 & 3.1755 & 3.2416 & 3.1974 \\ \hline \end{array}\]
请自己编写算法程序, 不要直接调用软件包中的拟合命令(但你可以用软件包来验证你程序写得是否正确), 回答下列问题.
(1)利用四次多项式$p(x)$进行最小二乘拟合, 计算拟合多项式$p(x)$的表达式和误差
\[\varepsilon=\left(\sum\limits_{i=0}^{10}(p(x_i)-f(x_i))^2\right)^{\frac{1}{2}}.\]
保留六位有效数字.
(2)利用如下形式的$p(x)$进行拟合:
\[p(x)=a_0+a_1\sin(a_2x)+a_3\cos(a_4x).\]
这里$a_0,a_1,a_2,a_3,a_4$是参数, 参数的近似值为
\[a_0\approx 1.3, a_1\approx 2.2, a_2\approx 1.1, a_3\approx 0.9, a_4\approx 1.8.\]
计算拟合函数$p(x)$的表达式使得误差
\[\varepsilon=\left(\sum\limits_{i=0}^{10}(p(x_i)-f(x_i))^2\right)^{\frac{1}{2}}.\]
达到最小, 保留三位有效数字.