DFT用于音频信号处理
离散Fourier变换在信号处理中应用广泛. 我们下面探究离散Fourier变换在音频处理中的应用.
用Python作DFT的基本操作
Python的Numpy包内置了Fourier变换和快速Fourier变换(FFT)算法.
利用np.fft.fft(x)可以求出向量$x$的离散Fourier变换.
利用np.fft.ifft(y)可以求出向量$y$的逆离散Fourier变换.
导入音频数据文件
文件piano_data.csv包含了一个持续一秒钟的中央C调(262Hz)钢琴音符的音频数据(波幅, amplitude), 存储为一个长度为44100的向量(它的音频采样率是44100Hz, 即一秒钟采样44100次). 如果你要调用这个文件, 那么就需要把你的python文件和这个csv文件放在同一个文件夹中. 调用方式是
import numpy as np
data = np.loadtxt('piano_data.csv', delimiter=',')
time = np.linspace(0.0, 1.0, len(data)) #Data represents 1 second of audio
print("CSV has a vector of size =", data.shape)
可以用np.savetxt把numpy数组存储为一个txt文件 (如果我们要处理的音频文件比较大, 适宜采用分段的方式处理, 这时分段保存在本地就很重要.).
我们可以把data存储为一个音频文件, 存储方式是
import scipy.io.wavfile as wavfile
samplerate = 44100
wavfile.write('my_audio.wav', samplerate, np.real(data))
泛音
画出音频数据的离散Fourier变换的前1000个分量的幅值(magnitude)的折线图, 可以看到在262Hz会有一个凸起. 而其他频率处的凸起称为泛音(overtone). 不同的乐器听起来不一样(即使在同一个频率的音符也不一样), 是因为它们有不同的泛音.
import matplotlib.pyplot as plt #用Python画图就需要调用pyplot包
x = np.linspace(1,1000,1000)
fig = plt.figure()
plt.xlabel(r'$n$')
plt.ylabel(r'Magnitude of FFT')
plt.plot(x,np.abs(FFTdata[0:1000]))
plt.scatter(262,np.abs(FFTdata[262]),c = 'r',marker = 'o') #262Hz处的凸起用红点描出
plt.show()
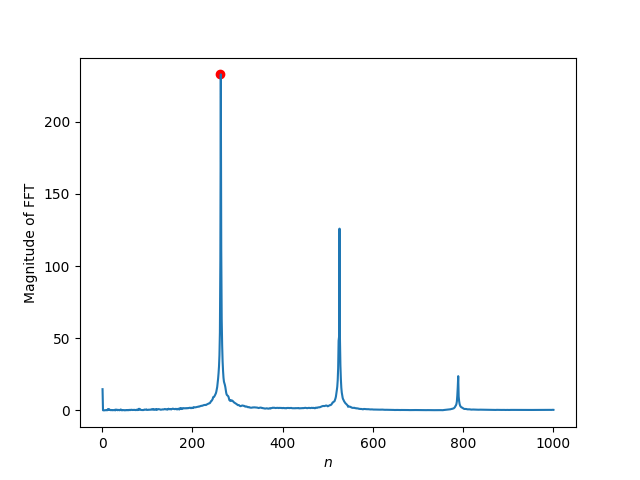
图1:音频数据的DFT的前1000个分量的幅值的折线图
用DFT去噪
添加随机噪声
下面我们用离散Fourier变换来对音频数据去噪. 首先我们先对原始的音频数据添加一些随机噪声.
把有噪声的音频数据保存为音频文件听一下有什么效果.
如果你的电脑无法播放wav文件, 可以上网寻找wav转mp3的在线工具. 比如这里
np.random.seed(0)
noisy_data = data + 0.005 * np.random.randn(len(data))
#作Fourier变换
FFTnoisy = np.fft.fft(noisy_data)
#保存噪声到本地, 地址可自行修改
wavfile.write('myaudio_noisy.wav', samplerate, np.real(noisy_data))
画出原始音频数据(data)和添加了噪声之后的音频数据(noisy_data)的离散Fourier变换的前1000个分量的幅值, 可以看到添加噪声后的音频数据在262Hz处有凸起, 在其他地方也会有少量的幅值(但远大于原始数据的幅值).
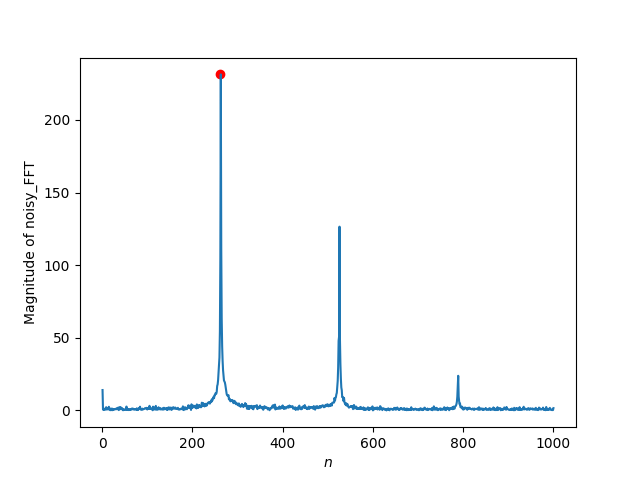
图2:带噪声音频数据的DFT的前1000个分量的幅值的折线图
去除噪声
下面去除noisy_data中的噪声. 选取一个基准幅值(记为$K$), 如果离散Fourier变换在某个频率处的幅值比$K$小, 则把该频率处的幅值设为$0$, 然后作逆Fourier变换得到“降噪”之后的音频数据(记为denoised_data). 画出denoised_data的离散Fourier变换的前1000个分量的幅值, 把降噪后的音频数据保存为音频文件, 听一听有什么效果. 可以听出杂音明显少了很多.
K = 3 #取基准幅值为3. 可以把3改成其他数试试看会有什么效果.
for i in range(data.shape[0]):
if(np.abs(FFTnoisy[i]) < K): #把幅值小于3的频率的幅值都变成0
FFTnoisy[i] = 0
IFFTnoisy_data = np.fft.ifft(FFTnoisy) #得到去噪后的音频数据
wavfile.write('myaudio_denoised.wav', samplerate, np.real(IFFTnoisy_data))
#把去噪后的音频保存到本地
比较去噪后的音频数据denoised_data和原始音频数据data的误差, 即把两个44100维向量作差, 观察一下它的2-范数.
| 原始数据和带噪声数据之间的误差 | 1.0451029075185467 |
| 原始数据和去噪后数据之间的误差 | 0.27836999052434663 |
下面的代码是画出音频数据前200次采样的波形图.
fig = plt.figure()
plt.xlabel(r'$t$')
plt.ylabel(r'Amplitude')
plt.plot(time[0:200],data[0:200], c = 'b')
plt.plot(time[0:200],noisy_data[0:200], c = 'g')
plt.plot(time[0:200],IFFTnoisy_data[0:200], c = 'r')
plt.show()
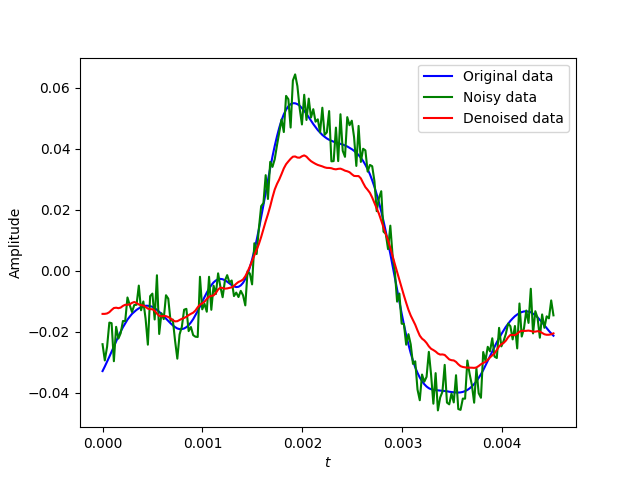
图3:前200次采样(约$0.0045$秒)的波形图. 纵坐标为波幅(amplitude).