参考书：Rainer Kress, Numerical Analysis(GTM181), Section11.4.

问题

我们已经研究了求解两点边值问题

的数值解法了. 下面, 我们考虑下面更一般的情况(称为Sturm-Liouville问题)

并假设$p\in C^1[a,b]$, $q,r\in C[a,b]$, $p(x)>0$, $q(x)\ge 0$, $\forall x\in[a,b]$.

为方便起见, 我们记

对方程$(1.2)$两边同乘一个函数$v$, 其中$v\in C_0^1[a,b]$. 然后用分部积分, 可知问题$(1.2)$的解$u$满足

其中,

是一个双线性函数(sesquilinear function), 并且

我们把$(1.3)$叫做问题$(1.2)$的弱形式(weak formulation)或者变分形式(variational formulation).

反之, 若$u\in C^2[a,b]$满足$(1.3)$, 根据分部积分可得

对任意$v\in C_0^1[a,b]$都成立. 利用数学分析的知识可以证明, 此时$u$必定满足$(1.2)$.

习题

假设$u\in C^2[a,b]$. 若$(1.5)$式对任意$v\in C_0^1[a,b]$成立, 证明: $u$满足$(1.2)$式.

弱解

$L^p$空间

我们把定义在区域$\Omega$上的可积函数$f:\Omega\to\mathbb{R}$的全体记为$L^1(\Omega)$.

一般“可积函数”都是指Lebesgue可积函数. 同学们如果没学过实变函数, 可以暂时先默认$f$是Riemann可积函数, 对后续的理解不会有太大影响.

受制于课程安排, 我们不过多介绍Lebesgue可积函数的定义. 我们这里约定可积函数$f\in L^1(\Omega)$就是满足下式的可测函数$f$的全体:

\[\int_{\Omega}\vert f(x)\vert\mathrm{d}x < \infty.\]

关于可测函数的概念, 也在实变函数中. 为方便理解, 暂时先把“可测函数”当成一般的函数即可.

若$f\in L^1(\Omega)$, 我们定义$L^1$-范数如下:

类似可以引入$L^p$-范数为

除此之外, 也可以引入$L^p(\Omega)$空间, 定义为满足下式的可测函数全体:

Sobolev空间

动机

我们这里只是简单介绍一元情形的Sobolev空间, 关于一般情形, 下个学期在偏微分方程课上会讲.

注意到, 只要$u\in C^1[a,b]$, 那么$(1.4)$式就有意义(但$(1.2)$式需要有二阶导数). 事实上, 这等价于求$u,u’\in L^1(a,b)$, 其中$u’$的具体含义还不确定. 我们就暂时把满足$(1.3)$式的$C^1$函数$u$称为问题$(1.2)$的弱解(weak solution). 而问题$(1.2)$本身的真解叫做经典解(classical solution).

变分方法(variational approach)的主要步骤:

• (1)需要明确指出“弱解”的定义, 这需要引入一个最基本的工具——Sobolev空间.
• (2)用Lax-Milgram定理给出弱解的存在性和唯一性.
• (3)弱解的正则性(regularity), 即能否提升它的光滑程度, 比如到$C^2$.
• (4)通过证明弱解是$C^2$的, 来说明该弱解也是经典解.

其中, 这里的步骤(4)我们已经在前面的习题部分验证过了.

定义

设$I=(a,b)$是开区间(可以取无穷), $p\in\mathbb{R}$满足$1\le p\le\infty$,

Definition

把Sobolev空间 $W^{1,p}(I)$定义为

\[W^{1,p}(I)=\left\{u\in L^p(I):\exists g\in L^p(I),\text{使得}\int_Iuv'=-\int_Igv, \forall v\in C_c^1(I)\right\}.\]

对上述$u\in W^{1,p}(I)$与$g$, 我们记$u’=g$, 叫做$u$的弱导数.

对于$p=2$的情形, 我们记

\[\boxed{H^1(I)=W^{1,2}(I)}\]

在上述定义中, 我们把$v$称为检验函数(test function).

事实上, Sobolev空间中也有Newton-Leibniz公式: 若$u\in W^{1,p}(I)$, 则

Example

例1. 对任意$1\le p\le\infty$, 函数$u(x)=\vert x\vert$属于$W^{1,p}(-1,1)$, 并且$u’=g$,

其中,

\[g(x)=\left\{\begin{aligned} &1, &&0 < x < 1, \\ &-1, &&-1 < x < 0. \end{aligned}\right.\]

但是对任意的$1\le p\le\infty$, $g$不属于$W^{1,p}(-1,1)$.

Important Remark

到目前为止, 希望这个例子可以让你理解为何要引入Sobolev空间: 我们知道, $u(x)=\vert x\vert$在$0$附近并不是可微函数, 所以不可能有$u\in C^1$. 然而, $u$的弱导数却是存在的, 因此$u\in W^{1,p}$.

在后面, 我们引入的Galerkin方法主要就是用分片线性函数来逼近问题$(1.2)$的解, 为了处理分片线性函数的小区间端点的不可微性, 我们采用的方法就是利用Sobolev空间的工具.

我们把$W^{1,p}(I)$的范数定义为

当$p=2$时, 定义

可以证明, $L^2(I)$和$H^1(I)$都是Hilbert空间.

在泛函分析中, Hilbert空间指完备的赋范线性空间, 这里不过多介绍.

为方便理解, 在接下来的学习中, 我们只需要知道Hilbert空间是内积空间就够了,

$L^2$内积定义为

\[(u,v)_{L^2}=\int_Iu(x)v(x)\mathrm{d}x,\]

而$H^1$内积定义为

\[(u,v)_{H^1}=(u,v)_{L^2}+(u',v')_{L^2}.\]

我们可以证明如下事实，它的证明需要一些实变函数的知识, 略. 我们只需要知道它是对的即可.

$H^1[a,b]$是$C[a,b]$的子集.

下面给出问题$(1.2)$弱解的正式定义. 记

Definition

问题$(1.2)$的弱解(weak solution), 指的是函数$u\in H_0^1[a,b]$, 满足$(1.3)$式对任意$v\in H_0^1[a,b]$都成立.

问题$(1.2)$存在唯一弱解$u$, 且满足

\[\|u\|_{H^1}\le\dfrac{1}{c}\|r\|_{L^2}.\]

证明： 由$(1.4)$以及Cauchy-Schwarz不等式, 双线性函数$S$满足如下的连续性(continunity)估计:

由Newton-Leibniz公式以及Cauchy-Schwarz不等式,

所以对任意$u\in H_0^1[a,b]$, 双线性函数$S$满足如下的强制性(coerciveness)估计:

其中, $c$是个常数.

(1)若$u_1,u_2\in H_0^1[a,b]$都是问题$(1.2)$的弱解, 则

取$v = u_1-u_2$, 则

于是$u_1-u_2=0$, 从而问题$(1.2)$存在唯一的弱解.

(2)由于$u$是问题$(1.2)$的弱解, 于是

根据Cauchy-Schwarz不等式可得

可得

约去一个$\vert\vert u\vert\vert_{H^1}^2$即可得到欲证不等式. $\square$

弱解是经典解

前面定义问题$(1.3)$的解是问题$(1.2)$的弱解. 我们来证明问题$(1.3)$的解$u\in H_0^1[a,b]$ 也是经典解.

定义

则$f\in C^1[a,b]$. 由$(1.2)$, 利用分部积分可得

令

以及

则$v_0\in H_0^1[a,b]$并且

所以$pu’=f+c$. 由于$f,p\in C^1[a,b]$并且$p(x)>0$恒成立, 则$u’\in C^1[a,b]$并且

这就完成了证明. $\square$

Galerkin方法

到目前为止, 即使你依然不太理解前面的弱解的概念, 你只需要知道: 求解问题$(1.2)$等价于求解问题$(1.3)$, 即可. 本节我们着重研究用数值方法来求问题$(1.3)$的解.

下面记$V = H_0^1[a,b]$. 假设$[a,b]$有如下的等距剖分（分成了$n+1$等分）:

其中$\lbrace x_i\rbrace$为结点, $x_{i}-x_{i-1}=h=\dfrac{b-a}{n+1}$.

我们用$\mathcal{M}_h$上的连续的分段线性函数(一次样条函数)来逼近$u(x)$. 引入逼近空间

显然, $V_h\subset V$. 我们把问题$(1.3)$改写为如下的离散形式:

注意, 对于函数$u_h\in V_h$, 只要我们确定$u_h$在$x_1,x_2,\cdots,x_{n}$的值, 那么就可以确定函数$u_h$的表达式. 所以$V_h$是一个$n$维线性空间. 问题$(1.5)$相当于用有限维空间来逼近原问题的解. 我们把问题$(1.5)$称为问题$(1.3)$的Galerkin方法.

由于$V_h$是$n$维线性空间, 所以存在一组基$\lbrace \phi_1,\cdots,\phi_n\rbrace$, 于是任意$u_h\in V_h$都可以表示为

如何求其中的系数$u_1,\cdots,u_n$? 我们想办法把已知条件变成一个线性方程组的形式. 取$v_h = \phi_j$, $j=1,2,\cdots,n$, 可得下面的关于未知数$u_1,\cdots,u_n$的方程组:

如果我们记

以及

然后定义刚度矩阵(stiffness matrix)是 $K=(k_{ij})\in\mathbb{R}^{n\times n}$, 右端向量(load vector)为 $F=(f_i)\in\mathbb{R}^{n\times 1}$, 解向量为 $U = (u_i)_{n\times 1}\in\mathbb{R}^{n\times 1}$, 那么方程组$(1.6)$可以改写为矩阵向量的形式:

综上所述, 利用$(1.7)$式求出$u_1,\cdots,u_n$之后, 就知道Galerkin离散后的问题$(1.5)$的解(即原问题的数值解)了.

下面, 一个很自然的问题产生了：如何选取基函数$\lbrace \phi_k\rbrace_{k=1}^n$, 使得问题$(1.5)$求解更加方便?

$\phi_k$是结点基函数——有限元方法

如果我们采取结点基函数(nodal basis), 即$\phi_k\in V_h$满足

这时问题就变成了一种最简单的有限元方法(Finite element method). 此时$\phi_i(1\le i\le n)$的表达式为

于是,

即此时$u_j$的值就是原问题真解在$x_j$处的近似值. 现在的关键是要求出线性方程组$(1.7)$的矩阵$K$和向量$F$.

记$p_j=p(x_j), q_j=q(x_j), r_j=r(x_j)$, 它们都是可以预先计算出来的.

$p,q$都是常数

若$p,q$都是常数, 我们可以直接计算出各个区间$[x_{i-1},x_i]$上的单元刚度矩阵$K^i=(k_{lm}^i)_{2\times 2}:$

因此, 把各个区间的单元刚度矩阵加在一起可得总刚度矩阵$K$.

$p,q$不是常数

若$p,q$都不是常数, 那就需要用数值积分来处理$k_{ij}$了. 各个区间$[x_{i-1},x_i]$上的单元刚度矩阵$K^i=(k_{lm}^i)_{2\times 2}$可以用数值积分计算. 首先,

于是, 采用Simpson公式的计算方法如下: (同学们也可以考虑改为用Gauss积分或者其他更高精度的数值积分方式来计算. )

右端向量

右端向量用Simpson公式处理得到

数值例子

考虑问题

其中$f(x)=2\pi^2\sin(\pi x)$. 这个问题的真解是$u(x)=\sin(\pi x).$ 编写程序实现在$n$个小区间构成的等距网格上使用有限元方法求问题$(1.8)$的数值解.

运行结果如下：

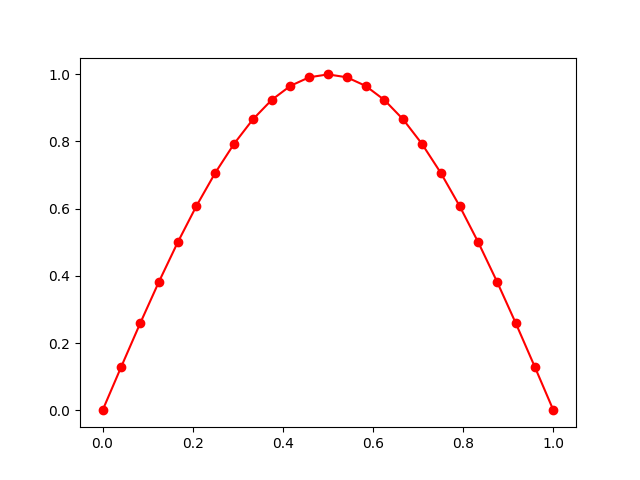
图：问题$(1.8)$的数值解.

Python代码如下:

import numpy as np
import scipy.sparse as sparse
from scipy.sparse.linalg import spsolve
import matplotlib.pyplot as plt

def Elliptic1D(p, q, r, N):
    """
    Solving equation -(pu')'+qu=r, u(-1)=u(1)=0. 
    Input arguments:
    p: parameter p in the equation. 
    q: parameter q in the equation.
    r: a function.
    N: number of subintervals.
    """
    h = 1.0/N
    x = np.linspace(0,1,N+1)

    # Stiffness matrix
    a12 = -p/h+q*h/6    #a_{j+1,j} 
    a11 = 2*p/h + 2*q*h/3 #a_{j,j}
    K = sparse.lil_matrix((N-1,N-1))
    for i in range(N-1):
        K[i,i] = a11
    for i in range(N-2):
        K[i,i+1] = a12
        K[i+1,i] = a12
        
    # Load vector
    R = r(x) # vector r
    F = np.zeros(N-1)
    for i in range(N-1):
        F[i] = h/6.0*(R[i]+4*R[i+1]+R[i+2])
    
    # Solving
    KK = sparse.csc_matrix(K)
    U = spsolve(KK,F)

    UU = np.zeros(N+1)
    UU[1:N] = U
    return UU

if __name__ == "__main__": 
    N = 24
    p = 1
    q = np.pi*np.pi

    def r(x):
        return 2*np.pi*np.pi*np.sin(np.pi*x)
    
    UU = Elliptic1D(p,q,r,N)

    #Plotting
    x = np.linspace(0,1,N+1)
    plt.plot(x, UU, 'ro-')
    plt.show()

Matlab代码如下:

function UU = Elliptic1D(p, q, r, N)
    %%
    % Solving equation -(pu')'+qu=r, u(-1)=u(1)=0. 
    % Input arguments:
    % p: parameter p in the equation. 
    % q: parameter q in the equation.
    % r: a function.
    % N: number of subintervals.
    
    h = 1.0/N;
    x = linspace(0,1,N+1);

    % Stiffness matrix
    a12 = -p/h + q*h/6;
    a11 = 2*p/h + 2*q*h/3;
    e = ones(N-1,1);
    K = spdiags([a12*e a11*e a12*e],-1:1,N-1,N-1);

    % Load vector
    R = r(x);
    F = zeros(N-1,1);
    for i = 1:N-1
        F(i)=h/6.0*(R(i)+4*R(i+1)+R(i+2));
    end

    % Solving
    U = K\F;
    UU = [0; U; 0];
end

% 主程序
N = 24;
p = 1;
q = pi*pi;

r = @(x) 2*pi*pi*sin(pi*x);

UU = Elliptic1D(p,q,r,N);

%Plotting
x = linspace(0,1,N+1);
figure(1)
plot(x, UU, 'ro-')

误差分析

对任意函数$g\in C^1[a,b]$满足$g(a)=0$, 都有

由Cauchy-Schwarz不等式,

两边关于$x$积分, 可得Friedrichs不等式

后面作误差分析时我们要用到这个不等式.

Lemma

设$f\in C^2[a,b]$, $L_1f$表示$f$在$[a,b]$上的Lagrange线性插值函数, 余项记为$R_1f:=f-L_1f$. 则有如下估计:

\[\begin{aligned} & \|R_1f\|_{L^2} \le (b-a)^2\|f''\|_{L^2}, \\ & \|(R_1f)'\|_{L^2} \le (b-a)\|f''\|_{L^2}. \end{aligned}\]

证明: 利用Lagrange插值函数的性质, $(R_1f)(a)=(R_1f)(b)=0$, 由分部积分可得

由Cauchy-Schwarz不等式可得

对$g=R_1f$利用Friedrichs不等式即可得欲证结论. $\square$

($H^1$估计) 设$u_h$是有限元方法在小区间长度为$h$时的数值解, $u$是原问题的真解. 则有如下估计:

\[\|u_h-u\|_{H^1} \le C\|u''\|_{L^2}h,\]

其中, $C$是常数.

($L^2$估计) 设$u_h$是有限元方法在小区间长度为$h$时的数值解, $u$是原问题的真解. 则有如下估计:

\[\|u_h-u\|_{L^2} \le C\|u''\|_{L^2}h^2,\]

其中, $C$是常数.

$\phi_k$是正交函数——谱方法

如果我们把$V_h$设为由一些关于权函数$w(x)$的正交函数张成的空间, 即$\phi_k\in V_h$满足

那么这时就得到谱方法(spectral method). 例如,

• $\phi_k(x)=e^{ikx}$ (Fourier谱方法)
• $\phi_k(x)=T_k(x)$ (Chebyshev谱方法)
• $\phi_k(x)=L_k(x)$ (Legendre谱方法)
• $\phi_k(x)=\mathscr{L}_k(x)$ (Laguerre谱方法)
• $\phi_k(x)=H_k(x)$ (Hermite谱方法)

其中, $T_k,L_k,\mathscr{L}_k,H_k$分别是$k$次Chebyshev, Legendre, Laguerre, Hermite多项式.

多项式谱方法

由于篇幅原因, 我们另开一个页面来介绍多项式谱方法, 请点击这里作跳转.

Fourier谱方法

Fourier谱方法需要用到离散Fourier变换. 关于Fourier谱方法, 请点击这里作跳转.

习题

习题一

计算问题$(1.8)$在$n=8,16,32,64,128,256,512,1024$时数值解与真解误差的$L^2(\Omega)$范数, 并求出误差阶. (提示: $L^2$范数可用数值积分计算)

习题二

修改前面程序中的Elliptic1D函数, 补全下面的TODO部分, 使得当$p,q$是函数的情形也能调用. (在python和matlab中二选一即可)

Python代码

def Elliptic1D(p, q, r, N):
    """
    Solving equation -(pu')'+qu=r, u(-1)=u(1)=0. 
    Input arguments:
    p: parameter p in the equation. 
    q: parameter q in the equation.
    r: a function.
    N: number of subintervals.
    """
    h = 1.0/N
    x = np.linspace(0,1,N+1)

    # Stiffness matrix
    K = sparse.lil_matrix((N-1,N-1))
    if(callable(p)==False): #p是常数，直接计算刚度矩阵
        a12 = -p/h  #a_{j+1,j}
        a11 = 2*p/h #a_{j,j}
        for i in range(N-1):
            K[i,i] = a11
        for i in range(N-2):
            K[i,i+1] = a12
            K[i+1,i] = a12
    else:   #p是函数，用数值积分来计算刚度矩阵
        #TODO: 把下面的pass换成相应的代码.
        pass

    if(callable(q)==False): #q是常数，直接计算刚度矩阵
        b12 = q*h/6    #a_{j+1,j} 
        b11 = 2*q*h/3  #a_{j,j}
        for i in range(N-1):
            K[i,i] += b11
        for i in range(N-2):
            K[i,i+1] += b12
            K[i+1,i] += b12
    else:  #q是函数，用数值积分来计算刚度矩阵
        #TODO: 把下面的pass换成相应的代码.
        pass
        
    # Load vector
    R = r(x) # vector r
    F = np.zeros(N-1)
    for i in range(N-1):
        F[i] = h/6.0*(R[i]+4*R[i+1]+R[i+2])
    
    # Solving
    KK = sparse.csc_matrix(K)
    U = spsolve(KK,F)

    UU = np.zeros(N+1)
    UU[1:N] = U
    return UU

Matlab代码

function UU = Elliptic1D(p, q, r, N)
    %%
    % Solving equation -(pu')'+qu=r, u(-1)=u(1)=0. 
    % Input arguments:
    % p: parameter p in the equation. 
    % q: parameter q in the equation.
    % r: a function.
    % N: number of subintervals.
    
    h = 1.0/N;
    x = linspace(0,1,N+1);

    % Stiffness matrix
    K = sparse(N-1,N-1);
    if(isa(p, 'function_handle') == 0) %p是常数，直接计算刚度矩阵
        a12 = -p/h;
        a11 = 2*p/h;
        e = ones(N-1,1);
        K = K + spdiags([a12*e a11*e a12*e],-1:1,N-1,N-1);
    else %p是函数，用数值积分来计算刚度矩阵
        % TODO: 把下面else的部分换成相应的代码.
    end

    if(isa(q, 'function_handle') == 0) %p是常数，直接计算刚度矩阵
        b12 = q*h/6;
        b11 = 2*q*h/3;
        e = ones(N-1,1);
        K = K + spdiags([b12*e b11*e b12*e],-1:1,N-1,N-1);
    else %q是函数，用数值积分来计算刚度矩阵
        % TODO: 把下面else的部分换成相应的代码.
    end

    % Load vector
    R = r(x);
    F = zeros(N-1,1);
    for i = 1:N-1
        F(i)=h/6.0*(R(i)+4*R(i+1)+R(i+2));
    end

    % Solving
    U = K\F;
    UU = [0; U; 0];
end

习题三

考虑问题

其中$f(x)=(\frac{1}{4}\pi^2+1)\sin(\frac{1}{2}\pi x)+\frac{1}{2}\pi\cos(\frac{1}{2}\pi x)$.

这个问题的真解是$u(x)=\sin(\frac{1}{2}\pi x).$

1. 注意这个问题并不是零边值问题. 求一个特解$G$满足

2. 写出问题$(1.9)$的弱形式

其中, $V=H_0^1(\Omega)$, 并且

(注意, 此时$a$并不是对称的双线性函数. )

3. 编写程序实现在$n$个小区间构成的等距网格上使用有限元方法求问题$(1.9)$的数值解.

4. 画出$n=8$时的数值解, 计算$n=8,16,32,64,128,256,512,1024$时数值解与真解误差的$L^2(\Omega)$范数, 并求出误差阶. (提示: $L^2$范数可用数值积分计算)

5.(*) 能否用理论证明第4问中的误差阶确实是你做数值试验观察到的那样?

习题四

考虑混合边界问题

1. 验证这个问题的变分形式为: 求$u\in V$使得

其中

2. 证明当$f\in C^0[a,b]$时, 这个问题存在唯一的弱解.

3. 把区间分成$n$等份. 定义有限元空间

请写出结点基函数的表达式.

(注意: $\phi_1,\cdots,\phi_{n-1}$与前面都是一样的, 但在$\phi_n$处的结点基函数与前面稍微不一样. )

4. 给出刚度矩阵$K$的计算公式, 建立线性方程组.

5. 考虑$f(x)=\left(\dfrac{\pi^2}{4}+1\right)\sin\dfrac{\pi x}{2}$, 此时真解为$u(x)=\sin\dfrac{\pi x}{2}$.

• (1) 编写程序实现在$n$个小区间构成的等距网格上使用有限元方法求问题$(1.10)$的数值解.

• (2) 画出$n=8$时的数值解, 计算$n=8,16,32,64,128,256,512,1024$时数值解与真解误差的$L^2(\Omega)$范数, 并求出误差阶. (提示: $L^2$范数可用数值积分计算)