设$\Omega\subset\mathbb{R}^n$为凸开集, $K\subset\Omega$为紧集. 证明: 存在常数$C$使得对任何定义在$\Omega$上的凸函数$F$(可能无界)皆有

\[\sup_K\vert F\vert \le C\int_{\Omega}\vert F\vert .\]

思路: 对$n\ge 1$, 定义在$\mathbb{R}^n$中的开集上的凸函数是连续函数. 设$x_0\in K$满足$\vert F(x_0)\vert =\sup\limits_{x\in K}\vert F(x)\vert $.

我们利用凸性进行上下界的放缩: 对任意$x\in B$($B$是$\Omega$的一个子集), 取合适的$y$使得

\[F(x_0) \le \lambda F(x) + (1-\lambda)F(y), \qquad \lambda\in(0,1),\]

其中$x_0 = \lambda x + (1-\lambda)y$即$y=\dfrac{x_0-\lambda x}{1-\lambda}$. 再取合适的$z$使得

\[F(x) \le \mu F(x_0) + (1-\mu) F(z),\]

其中$x = \mu x_0 + (1-\mu) z$, 即$z=\dfrac{x-\mu x_0}{1-\mu}$.

为方便起见, 我们可以取$\lambda=\mu=\dfrac{1}{2}$. 而我们需要保证$y,z$仍然落在$\Omega$中, 最简单的, 那我们就先考虑$x_0=0$的情形, 让$B$是一个球, 这样$y = -x\in B$, $z = 2x\in 2B$. 所以只需要取合适的半径$r$使得$B\subset 2B\subset\Omega$. 由于$K$是紧集而$\Omega$是开集, 所以$K$到$\partial\Omega$的距离大于$0$, 因此$r$直接定义为$K$到$\partial\Omega$的距离即可. 注意$\Omega$可能是$\mathbb{R}^n$, 这时为保证有限, 可以取

\[r=\min\lbrace \mathrm{dist}(K,\partial\Omega), 1\rbrace .\]

接下来把思路完善一下即可.

证明： 凸开集上的凸函数是连续函数. 设$x_0\in K$满足$\vert F(x_0)\vert =\sup\limits_{x\in K}\vert F(x)\vert $.

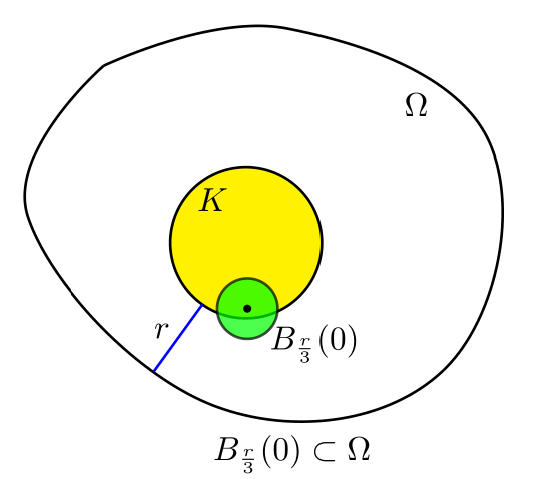
(1)不妨设$0\in K$, $x_0=0$. 取$r=\min\lbrace \mathrm{dist}(K,\partial\Omega), 1\rbrace $, 其中,

\[\mathrm{dist}(K,\partial\Omega) = \inf\limits_{x\in K}\mathrm{dist}(x,\partial\Omega).\]

表示$K$中的点到边界$\partial\Omega$的最小值. 并定义$B=B_{\frac{r}{3}}(0)$. 则$B\subset2B\subset \Omega$, 从而如果$x\in B$, 则$-x\in B$并且$2x\in 2B\subset\Omega$.

(把$K$向外扩$r$个单位长度, 得到$K_r = K + B_r(0)$, 那么$K_r\subset\overline{\Omega}$. )

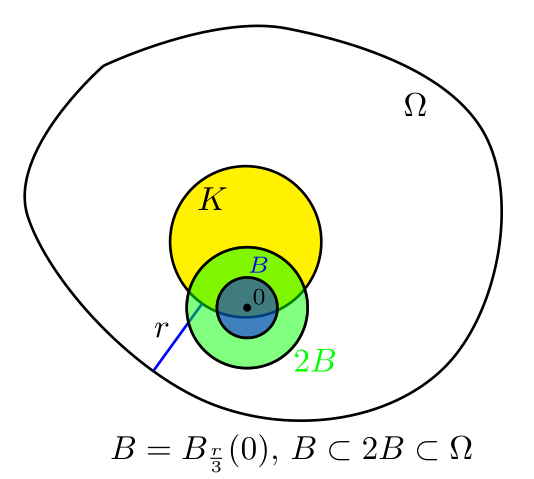
由于$F$是凸函数, 于是对任意$x\in B$, 有

\[\begin{aligned} &F(0) \le \dfrac{1}{2}F(x)+\dfrac{1}{2}F(-x), \\ &F(x) \le \dfrac{1}{2}F(0) + \dfrac{1}{2}F(2x). \end{aligned}\]

则

\[\begin{aligned} F(0)&=\dfrac{1}{\vert B\vert }\int_B\left(F(0)-\dfrac{1}{2}F(x)\right)\mathrm{d}x + \dfrac{1}{2\vert B\vert }\int_BF(x)\mathrm{d}x \\ &\le \dfrac{1}{2\vert B\vert }\int_BF(-x)\mathrm{d}x + \dfrac{1}{2\vert B\vert }\int_BF(x)\mathrm{d}x \\ &=\dfrac{1}{2\vert B\vert }\int_BF(x)\mathrm{d}x + \dfrac{1}{2\vert B\vert }\int_BF(x)\mathrm{d}x \\ &\le\dfrac{1}{\vert B\vert }\int_B\vert F(x)\vert \mathrm{d}x \le \dfrac{1}{\vert B\vert }\int_{\Omega}\vert F(x)\vert \mathrm{d}x. \end{aligned}\]

另一方面,

\[\begin{aligned} F(0)&=\dfrac{1}{\vert B\vert }\int_B\left(F(0)-2F(x)\right)\mathrm{d}x + \dfrac{2}{\vert B\vert }\int_BF(x)\mathrm{d}x \\ &\ge \dfrac{1}{\vert B\vert }\int_BF(2x)\mathrm{d}x + \dfrac{2}{\vert B\vert }\int_BF(x)\mathrm{d}x \\ &= \dfrac{1}{2^n\vert B\vert }\int_{2B}F(y)\mathrm{d}y + \dfrac{2}{\vert B\vert }\int_BF(x)\mathrm{d}x \\ &\ge -\dfrac{1}{2^n\vert B\vert }\int_{\Omega}\vert F(y)\vert \mathrm{d}y - \dfrac{2}{\vert B\vert }\int_{\Omega}\vert F(x)\vert \mathrm{d}x \\ &=-\dfrac{2^{-n}+2}{\vert B\vert }\int_{\Omega}\vert F(x)\vert \mathrm{d}x. \end{aligned}\]

综上,

\[\vert F(0)\vert \le \dfrac{2^{-n}+2}{\vert B\vert }\int_{\Omega}\vert F(x)\vert \mathrm{d}x.\]

(这里$\vert B\vert =\omega_n\left(\dfrac{r}{3}\right)^n$, 其中$\omega_n=\dfrac{\pi^{n/2}}{\Gamma(\frac{n}{2}+1)}$是$n$维单位球的体积. )

(2)对于最大值点$x_0$的一般情形($x_0$不一定是$0$), 考虑函数$G(x)=F(x+x_0)$, 定义域为$\Omega_0$, 其中$K_0=K-x_0=\lbrace x-x_0\vert x\in K\rbrace $, $\Omega_0=\Omega-x_0=\lbrace x-x_0\vert x\in\Omega\rbrace $. 于是, $0\in K_0$, 并且

\[\sup\limits_{x\in K}\vert G(x)\vert = \vert G(0)\vert .\]

注意$\mathrm{dist}(K_0,\partial\Omega_0)=\mathrm{dist}(K,\partial\Omega)$, 于是$r$的值可沿用在此处. 由(1)可得

\[\begin{matrix} \vert G(0)\vert &\le &\displaystyle\dfrac{2^{-n}+2}{\vert B\vert }\int_{\Omega_0}\vert G(x)\vert \mathrm{d}x \\ \| & & \| \\ \vert F(x_0)\vert & \le & \displaystyle\dfrac{2^{-n}+2}{\vert B\vert }\int_{\Omega_0}\vert F(x+x_0)\vert \mathrm{d}x & = \dfrac{2^{-n}+2}{\vert B\vert }\int_{\Omega}\vert F(y)\vert \mathrm{d}y \end{matrix}\]

最后作用了变换$y=x+x_0\in (\Omega-x_0)+x_0=\Omega$. 因此存在常数$C=\dfrac{2^{-n}+2}{\vert B\vert }$使得

\[\sup\limits_{x\in K}\vert F(x)\vert \le C\int_{\Omega}\vert F(x)\vert \mathrm{d}x.\]

这就完成了证明. $\square$

---