发布日期:2022年10月23日
参考文献:Hou, T.Y. (2003). Numerical Approximations to Multiscale Solutions in Partial Differential Equations. In: Blowey, J.F., Craig, A.W., Shardlow, T. (eds) Frontiers in Numerical Analysis. Universitext. Springer, Berlin, Heidelberg.
参考文献中包含许多笔误,我这里基本上都改过来了,方便大家的阅读. 另外有些翻译不准确的地方请大家指出,谢谢!
0 多尺度有限元方法的引入
求解下面的多尺度问题
\[\begin{aligned} &L_{\varepsilon}u:=-\nabla\cdot\left(a\left(\dfrac{x}{\varepsilon}\right)\nabla u\right)=f &&\text{ in }\Omega, &u=0 &&\text{ on }\Gamma=\partial\Omega, \end{aligned} \tag{1.9}\]其中$\Omega\subset\mathbb{R}^2$是凸多面体, $\varepsilon$是一个小的参数, $a(x)=\left(a_{ij}\left(\dfrac{x}{\varepsilon}\right)\right)_{i,j}$是对称的, 且满足
\[\alpha|\xi|^2\le \sum\limits_{i=1}^2\sum\limits_{j=1}^2 a_{ij}\xi_i\xi_j\le \beta|\xi|^2\]对任意$\xi\in\mathbb{R}^2$与$0 < \alpha < \beta$成立,
$a_{ij}(y)$关于$y$在$[0,1]^2$是光滑的周期函数, $f\in L^2(\Omega)$.
设$u_0$是均匀化问题的解:
\[\begin{aligned} &L_0u_0:=-\nabla\cdot(a^*\nabla u_0)=f, &&\text{ in }\Omega, &u=0 &&\text{ on }\Gamma, \end{aligned} \tag{1.10}\]其中
\[a^*=\langle a(y)(I+\nabla_y\chi(y))\rangle,\]并且$\chi(y)=(\chi^j(y))_{j=1}^n$是下面的cell problem的解:
\[\begin{aligned} &-\nabla_y\cdot(a(y))\nabla_y\chi^j)=\nabla_y\cdot(a(y)e_j), \qquad \text{ in }Y, \\ &\int_Y\chi^j(y)\mathrm{d}y=0. \end{aligned}\]由于$\Omega$是凸多面体, 则$u_0\in H^2(\Omega)$. 记$u_1(x,y)=\chi(y)\cdot \nabla_xu_0(x), $ 记$\theta_{\varepsilon}$是下面问题的解:
\[\begin{aligned} &L_{\varepsilon}\theta_{\varepsilon}=0, \qquad \text{ in }\Omega, \\ &\theta_{\varepsilon}(x)=u_1\left(x,\dfrac{x}{\varepsilon}\right), \qquad \text{ on }\Gamma, \end{aligned}\tag{1.11}\]接下来引入多尺度有限元方法. 设$\mathcal{T}_k$是$\Omega$的均匀三角剖分, $\lbrace x_j\rbrace _{j=1}^J$是$\mathcal{T}_h$的内部结点, $\lbrace \psi_j\rbrace _{j=1}^J$是标准线性有限元空间$W_h\subset H_0^1(\Omega)$的结点基. 设$S_i=\mathrm{supp}(\psi_i)$, 定义多尺度基函数$\phi^i$(支集在$S_i$中)如下:
\[L_{\varepsilon}\phi^i=0, \text{ in }K, \quad \phi^i=\psi_i \text{ on }\partial K, \forall K\in \mathcal{T}_h, K\subset S_i. \tag{1.12}\]显然, $\phi^i\in H_0^1(S_i)\subset H_0^1(\Omega)$. 令$V_h\subset H_0^1(\Omega)$表示由$\lbrace \phi^i\rbrace _{i=1}^J$张成的有限元函数空间.
我们引入下面的离散问题: 求$u_h\in V_h$使得
\[\left(a\left(\dfrac{x}{\varepsilon}\right)\nabla u_h, \nabla v_h\right) =(f,v_h), \qquad \forall v_h\in V_h. \tag{1.13}\]我们后面会指出, 在定义多尺度基函数的时候, 边界条件的选取对逼近多尺度问题的解起到重要作用. 直观上看, 多尺度基函数对应的边界条件会使得解在粗网格边界上产生振荡. 如果基函数选取线性的边界条件, 那么真解和有限元解在穿过有限元网格边界的时候产生一些错乱(mismatch). 后面我们会提出一个方法来解决这个问题.
1 误差估计$(h < \varepsilon)$
我们从Cea引理开始.
引理1(Cea) 设$u$是问题$(1.9)$的解, $u_h$是$(1.13)$的解. 则
\[\|u-u_h\|_{H^1(\Omega)}\le C\inf\limits_{v_h\in V_h}\|u-v_h\|_{H^1(\Omega)}.\]
证明: 这跟经典FEM的证明完全一样, 我们来复习一下. 首先, 由于我们考虑的是个椭圆问题, 即
\[\alpha|\xi|^2\le \sum\limits_{i=1}^n\sum\limits_{j=1}^n a_{ij}\xi_i\xi_j\le \beta|\xi|^2,\]其次, 利用Poincare-Friedrichs不等式可得对于$v\in H_0^1(\Omega)$, 有
\[(a(x/\varepsilon)\nabla v,\nabla v)\ge \alpha(\nabla v,\nabla v) =\alpha\int_{\Omega}|\nabla v|^2\mathrm{d}x\ge C\int_{\Omega}|v|^2\mathrm{d}x.\]由$(1.9)(1.13)$, 即对任意$v_h\in V_h$, 有
\[\begin{aligned} \left(a\left(\dfrac{x}{\varepsilon}\right)\nabla u, \nabla v_h\right)=(f,v_h), \\ \left(a\left(\dfrac{x}{\varepsilon}\right)\nabla u_h, \nabla v_h\right)=(f,v_h), \end{aligned}\]两式作差可得
\[\left(a\left(\dfrac{x}{\varepsilon}\right)\nabla (u-u_h), \nabla v_h\right)=0, \forall v_h\in V_h.\]特别地, 把上式$v_h$换成$u_h$也对. 所以
\[\left(a\left(\dfrac{x}{\varepsilon}\right)\nabla (u-u_h), \nabla (u-u_h)\right)= \left(a\left(\dfrac{x}{\varepsilon}\right)\nabla (u-u_h), \nabla (u-v_h)\right), \forall v_h\in V_h.\]则
\[\begin{aligned} \|u-u_h\|_{H^1(\Omega)}^2 &\le C\left(a\left(\dfrac{x}{\varepsilon}\right)\nabla (u-u_h), \nabla (u-u_h)\right) \\ &=C\left(a\left(\dfrac{x}{\varepsilon}\right)\nabla (u-u_h), \nabla (u-v_h)\right) \\ &\le C\|u-u_h\|_{H^1(\Omega)}\cdot \|u-v_h\|_{H^1(\Omega)}. \end{aligned}\]两边同除以$|u-u_h|_{H^1(\Omega)}$, 可得
\[\|u-u_h\|_{H^1(\Omega)}\le C\|u-v_h\|_{H^1(\Omega)}.\]上式对任意$v_h\in V_h$都成立, 在右边取下确界即可. $\square$
下面, 记$\Pi_h:C(\overline{\Omega})\to W_h\subset H_0^1(\Omega)$是通常的Lagrange插值算子:
\[\Pi_hu(x)=\sum_{j=1}^Ju(x_j)\psi_j(x), \qquad \forall u\in C(\overline{\Omega})\]并且$I_h:C(\overline{\Omega})\to V_h$是用多尺度基函数$\phi$作插值的插值算子
\[I_hu(x)=\sum_{j=1}^Ju(x_j)\phi^j(x), \qquad \forall u\in C(\overline{\Omega}).\]由多尺度基函数$\phi^i$的定义$(1.12)$, 我们有
\[L_{\varepsilon}(I_hu)=0, \text{ in }K, \quad I_hu=\Pi_hu, \text{ on }\partial K. \tag{1.14}\]这利用$L_{\varepsilon}$是线性算子就能马上得到.
引理2 设$u\in H^2(\Omega)$是问题(1)的解, 则存在与$h,\varepsilon$无关的常数$C$使得
\[\|u-I_hu\|_{L^2(\Omega)}+h\|u-I_hu\|_{H^1(\Omega)} \le Ch^2(|u|_{H^2(\Omega)}+\|f\|_{L^2(\Omega)}). \tag{1.15}\]
证明: 根据标准的有限元插值的结果, 可得
\[\|u-\Pi_hu\|_{L^2(\Omega)}+h\|u-\Pi_hu\|_{H^1(\Omega)}\le Ch^2|u|_{H^2(\Omega)}. \tag{1.16}\]另一方面, 由于在$\partial K$上满足$\Pi_hu-I_hu=0$, 并且有Poincare-Friedrichs不等式
\[\|v\|_{L^2(\Omega)}\le C\|\nabla v\|_{L^2(\Omega)}, \qquad \forall v\in H_0^1(\Omega),\]所以取$v=\Pi_hu-I_hu$并利用scaling argument(这里需要用到均匀剖分的条件), 可得
\[\|\Pi_hu-I_hu\|_{L^2(K)}\le Ch|\Pi_hu-I_hu|_{H^1(K)}, \qquad \forall K\in\mathcal{T}_h. \tag{1.17}\]下面我们估计上式右端. 首先, 在$(1.14)$两端同乘$I_hu-\Pi_hu\in H_0^1(K)$, 可得
\[\left(a(\tfrac{x}{\varepsilon})\nabla I_hu, \nabla(I_hu-\Pi_hu)\right)_K=0,\]其中$(\cdot,\cdot)_K$表示在$L^2(K)$上的$L^2$内积, 所以利用上式以及$(1.9)$可得
\[\begin{aligned} &\quad (a(\tfrac{x}{\varepsilon})\nabla(I_hu-\Pi_hu),\nabla(I_hu-\Pi_hu))_K \\ &=(a(\tfrac{x}{\varepsilon})\nabla(u-\Pi_hu), \nabla(I_hu-\Pi_hu))_K- (a(\tfrac{x}{\varepsilon})\nabla u, \nabla(I_hu-\Pi_hu))_K \\ &=(a(\tfrac{x}{\varepsilon})\nabla(u-\Pi_hu), \nabla(I_hu-\Pi_hu))_K-(f,I_hu-\Pi_hu)_K. \end{aligned}\]结合$(1.16)(1.17)$以及在问题定义中对$a(x/\varepsilon)$施加的椭圆条件, 可得
\[\begin{aligned} |I_hu-\Pi_hu|_{H^1(K)}&\le Ch|u|_{H^2(K)}+\|I_hu-\Pi_hu\|_{L^2(K)}\|f\|_{L^2(K)} \\ &\le Ch(|u|_{L^2(K)}+\|f\|_{L^2(K)}). \end{aligned} \tag{1.18}\]最后, 把$(1.16)(1.17)(1.18)$放在一起即可得最终结论. $\square$
定理3 设$u\in H^2(\Omega)$是问题$(1.9)$的解, $u_h\in V_h$是$(1.13)$的解, 则
\[\|u-u_h\|_{H^1(\Omega)}\le Ch\Big(|u|_{H^2(\Omega)}+\|f\|_{L^2(\Omega)}\Big).\]
证明: 由Cea引理和引理2可得
\[\|u-u_h\|_{H^1(\Omega)}\le C\|u-I_hu\|_{H^1(\Omega)} \le Ch\Big(|u|_{H^2(\Omega)}+\|f\|_{L^2(\Omega)}\Big).\]这就完成了证明. $\square$
由于$|u|_{H^2(\Omega)}=O(1/\varepsilon)$, 所以这个估计会有$O(\frac{h}{\varepsilon})$的误差, 在$\varepsilon\to 0$时误差会很大(blow up like $h/\varepsilon$)或者说没法收敛于$0$. (例如: 取$h=\varepsilon/2$. )
下一小节我们给出当$\varepsilon\to 0$时误差会趋于0的估计.
2 误差估计$(h>\varepsilon)$
本小节给出当$\varepsilon$趋于$0$时收敛结果关于$\varepsilon$也一致趋于$0$的误差估计, 我们首先列出本小节的主要定理, 这个定理跟传统FEM相比比较特殊(涉及到均匀化问题的解).
定理4 设$u\in H^2(\Omega)$是$(1.9)$的解, $u_h\in V_h$是$(1.13)$的解. 则
\[\|u-u_h\|_{H^1(\Omega)}\le C(h+\varepsilon)\|f\|_{0,\Omega} +C\left(\left(\dfrac{\varepsilon}{h}\right)^{\frac{1}{2}}+\varepsilon^{\frac{1}{2}}\right)\|u_0\|_{W^{1,\infty}(\Omega)}. \tag{1.19}\]其中, $u_0\in H^2(\Omega)\cap W^{1,\infty}(\Omega)$是均匀化问题$(1.10)$的解.
为了证明这个定理, 我们记
\[u_I(x)=I_hu_0(x)=\sum\limits_{j=1}^Ju_0(x_j)\phi^j(x)\in V_h,\]表示对均匀化问题的解用多尺度基函数插值得到的函数. 从$(1.14)$可得
\[L_{\varepsilon}(u_I)=0, \text{ in }K, \quad u_I=\Pi_hu_0, \text{ on }\partial K, \forall K\in\mathcal{T}_h.\]接下来的分析基于Moskow和Vogelius的如下引理:
引理5 设$u\in H^2(\Omega)$是问题$(1.9)$的解, $u_0\in H^2(\Omega)$是问题$(1.10)$的解, $\theta_{\varepsilon}\in H^1(\Omega)$是问题$(1.11)$ 的解, $u_1(x)=-\chi\left(\dfrac{x}{\varepsilon}\right)\cdot \nabla_xu_0(x), $ 则存在常数$C$与$u_0,\varepsilon,\Omega$无关, 使得
\[\|u-u_0-\varepsilon(u_1-\theta_{\varepsilon})\|_{H^1(\Omega)}\le C\varepsilon(|u_0|_{H^2(\Omega)}+\|f\|_{L^2(K)}).\]
由引理可知
\[\|u_I-u_{I0}-\varepsilon(u_{I1}-\theta_{I\varepsilon})\|_{H^1(K)}\le C\varepsilon|u_{I0}|_{H^2(K)}, \tag{1.20}\]其中, $u_{I0}$是$u_I$的有限元插值函数:
\[L_0u_{I0}=0\text{ in }K, \quad u_{I0}=\Pi_hu_0\text{ on }\partial K, \tag{1.21}\]$u_{I1}$满足关系式
\[u_{I1}(x,y)=-\chi^j(y)\dfrac{\partial u_{I0}}{\partial x_j}\text{ in }K, \tag{1.22}\]$\theta_{I\varepsilon}\in H^1(K)$是下面问题的解:
\[L_{\varepsilon}\theta_{I\varepsilon}=0\text{ in }K, \quad \theta_{I\varepsilon}(x) =u_{I1}(x,\tfrac{x}{\varepsilon})\text{ on }\partial K. \tag{1.23}\]根据$(1.21)$, 可得
\[u_{I0}=\Pi_hu_0\text{ in }K, \tag{1.24}\]即$u_{I0}$是线性函数, 从而$\vert u_{I0}\vert_{H^2(\Omega)}=0$, 即$(1.20)$的右端等于$0$.
利用椭圆正则性估计,
\[\|u_0\|_{H^2(\Omega)}\le C\|f\|_{L^2(\Omega)}.\]于是由引理5与$(1.20)$, 可得
\[\begin{aligned} \|u-u_I\|_{H^1(\Omega)} &\le \|(u-u_0-\varepsilon(u_1-\theta_{\varepsilon}))- (u_I-u_{I0}-\varepsilon(u_{I1}-\theta_{I\varepsilon})) \|_{H^1(\Omega)} \\ &\qquad +\|u_0+\varepsilon u_1-\varepsilon\theta_{\varepsilon} -u_{I0}-\varepsilon u_{I1}+\varepsilon\theta_{I\varepsilon}\|_{H^1(\Omega)} \\ &\le C\varepsilon\|f\|_{L^2(\Omega)}+\|u_0-u_{I0}\|_{H^1(\Omega)} +\|\varepsilon(u_1-u_{I1})\|_{H^1(\Omega)}+\|\varepsilon(\theta_{\varepsilon}-\theta_{I\varepsilon})\|_{H^1(\Omega)}. \end{aligned}\]接下来我们只需要分别估计右边各项.
引理6 我们有
\[\begin{gathered} \|u_0-u_{I0}\|_{H^1(\Omega)}\le Ch\|f\|_{L^2(\Omega)}, \\ \|\varepsilon(u_1-u_{I1})\|_{H^1(\Omega)}\le C(h+\varepsilon)\|f\|_{L^2(\Omega)}. \end{gathered}\]
证明: (1)首先,
\[\begin{aligned} \|u_0-u_{I0}\|_{H^1(\Omega)} &=\|u_0-\Pi_hu_0\|_{H^1(\Omega)} &&\text{(由(\ref{eq417})式)} \\ &\le Ch|u_0|_{H^2(\Omega)} &&\text{(由插值误差估计(\ref{eq408})式)} \\ &\le Ch\|f\|_{L^2(\Omega)} &&\text{(椭圆问题正则性)} \end{aligned}\](2)回顾:由于$\chi$满足
\[-\nabla_y\cdot(a(y))\nabla_y\chi^j)=\nabla_y\cdot(a(y)e_j),\]利用椭圆问题正则性估计可知$\chi^j\in H^2(Y)$. 利用Sobolev嵌入定理 [cf. Brezis, Functional Analysis, Sobolev Spaces and Partial Differential Equations, Thm8.8], 可得$\chi^j\in W^{1,\infty}(Y)$. 于是作一个scaling换元$x\mapsto x/\varepsilon$, 可知函数$\chi^j(x/\varepsilon)$满足
\[\|\chi^j\|_{L^{\infty}(\Omega)}+\varepsilon\|\nabla\chi^j\|_{L^{\infty}(\Omega)}\le C, \tag{1.25}\]其中常数$C$与$h,\varepsilon$无关. 因此对任意$K\in\mathcal{T}_h$, 有
\[\begin{aligned} \|\varepsilon(u_1-u_{I1})\|_{L^2(K)} &=\varepsilon\left\|\chi^j\dfrac{\partial}{\partial x_j}(u_0-\Pi_hu_0)\right\|_{L^2(K)} \\ \|\varepsilon\nabla(u_1-u_{I1})\|_{L^2(K)} &=\varepsilon\left\|\nabla\left(\chi^j\dfrac{\partial}{\partial x_j}(u_0-\Pi_hu_0)\right)\right\|_{L^2(K)} \\ &\le C\|\nabla(u_0-\Pi_hu_0)\|_{L^2(K)}+C\varepsilon|u_0|_{H^2(K)} \\ &\le C(h+\varepsilon)|u_0|_{H^2(K)}. \end{aligned}\]这就完成了证明. $\square$
引理7 我们有
\[\|\varepsilon\theta_{\varepsilon}\|_{H^1(\Omega)}\le C\sqrt{\varepsilon}\|u_0\|_{W^{1,\infty}(\Omega)}+C\varepsilon|u_0|_{H^2(\Omega)}.\]
证明: 定义$\zeta\in C_0^{\infty}(\mathbb{R}^2)$是一个cut-off function, 满足
\[\begin{aligned} \zeta\equiv 1, \text{ in }\Omega\setminus\Omega_{\delta/2}, \\ \zeta \equiv 0, \text{ in }\Omega_{\delta}, \\ 0\le\zeta\le 1, \text{ in }\mathbb{R}^2. \end{aligned}\]并且$\vert\nabla\zeta\vert\le\dfrac{C}{\delta}$在$\Omega$上成立. 其中, $\delta>0$是充分小的数, 并且
\[\Omega_{\delta}=\lbrace x\in\Omega:\mathrm{dist}(x,\partial\Omega)\ge\delta\rbrace .\]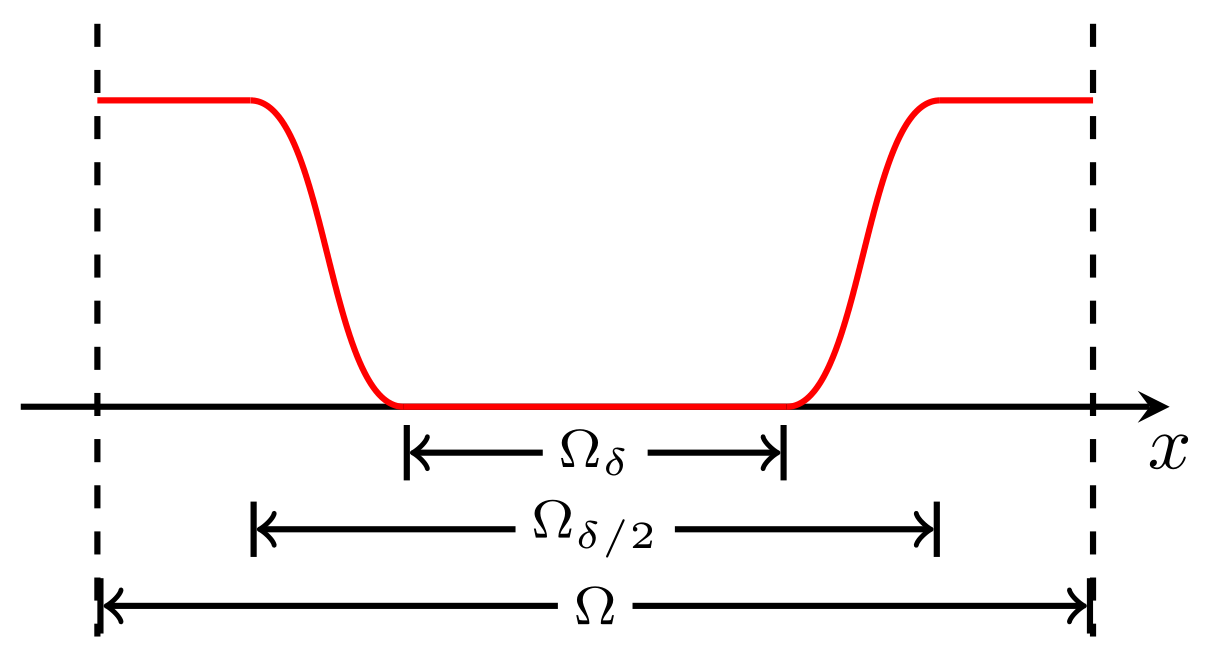
根据这个定义, 我们有$\theta_{\varepsilon}-\zeta u_1=\theta_{\varepsilon}+\zeta\chi\cdot\nabla_xu_0\in H_0^1(\Omega).$ 在方程$(1.11)$也就是$L_{\varepsilon}\theta_{\varepsilon}=0$两边同乘$\theta_{\varepsilon}-\zeta u_1$, 可得
\[\begin{aligned} &\left(a\left(\dfrac{x}{\varepsilon}\right)\nabla\theta_{\varepsilon}, \nabla\left(\theta_{\varepsilon}+\zeta\chi\cdot\nabla_xu_0\right)\right)=0, \\ \Leftrightarrow & \left(a\left(\dfrac{x}{\varepsilon}\right)\nabla\theta_{\varepsilon},\nabla\theta_{\varepsilon}\right) =-\left(a\left(\dfrac{x}{\varepsilon}\right)\nabla\theta_{\varepsilon},\nabla\left(\zeta\chi\cdot\nabla_xu_0\right)\right). \end{aligned}\]利用椭圆方程对系数的定义, 以及$(1.25)$, 从上式可推出
\[\begin{aligned} \|\nabla\theta_{\varepsilon}\|_{L^2(\Omega)} &\le C\|\nabla(\zeta\chi\cdot\nabla_xu_0)\|_{L^2(\Omega)} \notag \\ &\le C\|(\chi\cdot\nabla_xu_0)\nabla\zeta\|_{L^2(\Omega)} +C\left\|\zeta\sum\limits_{j=1}^n\nabla\chi^j\dfrac{\partial u_0}{\partial x_j}\right\|_{L^2(\Omega)} +C\left\|\zeta\sum\limits_{j=1}^n\chi^j\dfrac{\partial^2 u_0}{\partial^2 x_j}\right\|_{L^2(\Omega)} \notag\\ &\le C\sqrt{|\partial\Omega|\cdot\delta}\dfrac{D}{\delta} +C\sqrt{|\partial\Omega|\cdot\delta}\dfrac{D}{\delta}+C|u_0|_{H^2(\Omega)}. \end{aligned}\]其中, $D=|u_0|_{W^{1,\infty}(\Omega)}$, 第一个不等号用了前面一条居中式子, 第二个不等号用了求导的乘法法则, 第三个不等号是因为用$(1.25)$可知
\[\begin{aligned} \|(\chi\cdot\nabla_xu_0)\nabla\zeta\|_{L^2(\Omega)} &\le \|\chi\|_{L^{\infty}(\Omega)}\|\nabla\zeta\|_{L^2(\Omega)}\|\nabla_xu_0\|_{L^{\infty}(\Omega)} \notag \\ &\le C\cdot \left(\int_{\Omega_{\delta}\setminus\Omega_{\delta/2}}|\nabla\zeta|^2\right)^{\frac{1}{2}}\cdot \dfrac{D}{\delta}\notag \\ &\le C\sqrt{|\partial\Omega|\delta}\cdot\dfrac{D}{\delta} \end{aligned} \tag{1.27}\]另一项同理. (此处的$C$与$\Omega$无关!)
整理可得
\[\|\varepsilon\nabla\theta_{\varepsilon}\|_{L^2(\Omega)}\le C\left(\dfrac{\varepsilon}{\sqrt{\delta}}+\sqrt{\delta}\right)\|u_0\|_{W^{1,\infty}(\Omega)} +C\varepsilon|u_0|_{H^2(\Omega)}.\]由于$\delta>0$是任取的, 我们可以取$\delta=\varepsilon$即可.
另外, 根据极值原理得到
\[\|\theta_{\varepsilon}\|_{L^2(\Omega)} \le \|\chi\cdot\nabla_xu_0\|_{L^2(\partial\Omega)} \le C\|u_0\|_{W^{1,\infty}(\Omega)}.\]不可以根据Poincare-Friedrichs不等式得到
\[\|\varepsilon\theta_{\varepsilon}\|_{L^2(\Omega)} \le \varepsilon\|\nabla\theta_{\varepsilon}\|_{L^2(\Omega)} .\]因为$\theta_{\varepsilon}\notin H_0^1(\Omega)$.
所以结合上述两个不等式即可得到
\[\|\varepsilon\theta_{\varepsilon}\|_{H^1(\Omega)} \le C\sqrt{\varepsilon}\|u_0\|_{W^{1,\infty}(\Omega)}+C\varepsilon|u_0|_{H^2(\Omega)}.\]这就完成了证明. $\square$
引理8 我们有
\[\|\varepsilon\theta_{1\varepsilon}\|_{H^1(\Omega)} \le C\left(\left(\dfrac{\varepsilon}{h}\right)^{\frac{1}{2}}+\varepsilon^{\frac{1}{2}}\right)\|u_0\|_{W^{1,\infty}(\Omega)}.\]
证明: 首先回顾一下: $\theta_{I\varepsilon}\in H^1(K)$是下面问题的解:
\[L_{\varepsilon}\theta_{I\varepsilon}=0\text{ in }K, \quad \theta_{I\varepsilon}(x) =-\chi\left(\dfrac{x}{\varepsilon}\right)\cdot \nabla_x(\Pi_hx_0)\text{ on }\partial K.\]由极值原理,
\[\|\theta_{I\varepsilon}\|_{L^{\infty}(K)} \le \left\|\chi\left(\dfrac{x}{\varepsilon}\right)\cdot\nabla_x(\Pi_hx_0)\right\|_{L^{\infty}(\partial K)} \le C\|u_0\|_{W^{1,\infty}(K)}.\]所以
\[\|\varepsilon\theta_{I\varepsilon}\|_{L^2(\Omega)}\le C\varepsilon\|u_0\|_{W^{1,\infty}(\Omega)}.\](此处的$C$与常数$\Omega$无关)
另外, 利用类似$(1.27)$的推导可知
\[\begin{aligned} \|\varepsilon\nabla\theta_{I\varepsilon}\|_{L^2(K)} &\le C\varepsilon\|\Pi_hu_0\|_{W^{1,\infty}(K)}\left(\dfrac{\sqrt{|\partial K|}}{\sqrt{\delta}} +\dfrac{\sqrt{|\partial K|\cdot\delta}}{\varepsilon}\right)+C\varepsilon|\Pi_hu_0|_{H^2(K)} \\ &\le C\sqrt{h}\|u_0\|_{W^{1,\infty}(K)}\left(\dfrac{\varepsilon}{\sqrt{\delta}}+\sqrt{\delta}\right). \end{aligned}\]取$\delta=\varepsilon$, 最后得
\[\|\varepsilon\nabla\theta_{I\varepsilon}\|_{L^2(\Omega)} \le C\left(\dfrac{\varepsilon}{h}\right)^{\frac{1}{2}}\|u_0\|_{W^{1,\infty}(\Omega)}.\](根据均匀剖分, 把所有区域$K\in\mathcal{T}_h$的估计加起来之后会得到一个$\dfrac{1}{h}$项. )
结合两个不等式即可完成证明. $\square$
定理4的证明. 回到本小节的主要定理, 我们把上述引理以及Cea引理结合起来, 并利用正则性估计
\[\|u_0\|_{H^2(\Omega)}\le C\|f\|_{L^2(\Omega)}\]即可完成证明. $\square$
多尺度有限元方法的误差估计的右端确实是关于$\varepsilon\to 0$一致趋于$0$, 而传统FEM则是按$O(h^2/\varepsilon^2)$增长. 另一方面, 若$h\sim\varepsilon$, 则多尺度有限元方法的$H^1$误差和$L^2$误差都非常大, 我们把它叫做这个问题在网格尺度$h$与小尺度$\varepsilon$之间的“resonance effect”(共振效应?). 为了解决这个问题, 我们引入“过采样”(over-sampling)方法.