发布日期：2022年11月9日

GFEM用于多尺度问题

值得思考的问题:
引入限制算子$P$(以及它的特征函数)目的或者原理是什么? 在定义$d(S(n),\omega)$的时候, 我们可以把$Pu$改成$u$, 那这样子就跟$P$没关系了.
为什么必须要有$u_0=u^G+u^F$(即找局部特解然后求解$B(u^G,v)=F(v)-B(u^F,v)$)? 能否推广A-Harmonic的定义, 直接求解$B(u^0,v)=F(v)$？

GFEM用于多尺度问题

论文:

I. Babuška, R. Lipton, Optimal local approximation spaces for generalized finite element methods with application to multiscale problems, Multiscale Model. and Simul., SIAM, 9, 2011, 373–406.
I. Babuška, Robert Lipton, Paul Sinz, Michael Stuebner, Multiscale-Spectral GFEM and optimal oversampling, Computer Methods in Applied Mechanics and Engineering, Volume 364.

本文考虑用GFEM求解二阶椭圆偏微分方程, 且系数是$L^{\infty}(\Omega)$的. GFEM的构造方法是把$\Omega$分成许多小区域$\omega_i(i=1:m)$然后在每个小区域构造有限维逼近空间$\Psi_i$. 我们用了Kolmogorov $n$-width来确定最优的局部逼近空间, 这样的逼近空间在$\omega_i$上的逼近误差关于自由度$N_i$指数衰减. 而局部空间$\Psi_i$可以组成$H^1(\Omega)$的有限维子空间$S^N$, 然后用Galerkin方法来求数值解. 本文证明了Galerkin逼近误差也是关于$N$几乎指数衰减的.

$\S 2.1$ 问题构成

设$\Omega\subset\mathbb{R}^d$有$C^1$边界$\partial\Omega$. 我们考虑椭圆问题

\[-\mathrm{div}(A(x)\nabla u(x))=f(x), \forall x\in\Omega, \tag{2.1}\]

其中边界条件可以用Neumann边界条件:

\[n\cdot A\nabla u(x)=g, \qquad \forall x\in\partial\Omega, \tag{2.2}\]

或者Dirichlet边界条件

\[u(x)=g, \qquad \forall x\in\partial\Omega \tag{2.3}\]

在未来的工作中还会考虑混合边界条件以及非光滑边界的情况. 我们作如下的更多假设：

设$A(x)$是$d\times d$对称矩阵并且$a_{ij}(x)\in L^{\infty}(\Omega)$满足下面的强制性条件:

\[\alpha^\ast (x)\vert \boldsymbol{v}\vert ^2\le \boldsymbol{v}^tA(x)\boldsymbol{v}\le\beta^\ast (x)\vert \boldsymbol{v}\vert ^2, \qquad \forall x\in\Omega,\forall \boldsymbol{v}\in \mathbb{R}^d,\]

并且

\[0< \alpha\le\alpha^\ast (x)\le\beta^\ast (x)\le \beta < \infty, \quad \forall x\in\Omega.\]

我们把满足这个条件的所有系数记为$\mathfrak{C}$.

设$f\in H^k(\Omega)$, $k\ge 0$, $g\in H^{-\frac{1}{2}}(\partial\Omega)$, 并且在Neumann边界的条件下, 满足相容性条件

\[\int_{\partial\Omega}g\mathrm{d}s+\int_{\Omega}f\mathrm{d}s=0.\]

而在Dirichlet边界的条件下, $q\in H^{\frac{1}{2}}(\partial\Omega)$.

弱解$u\in H^1(\Omega)$存在. 在Dirichlet边界条件下, 解是唯一的. 而在Neumann边界条件下, 解在相差一个常数的情况下唯一. 由于我们只是假设了系数是可测的, 所以一般情况下对任意$\varepsilon>0$有$u\notin H^{1+\varepsilon}(\Omega)$.

我们现在要研究把GFEM用来逼近上述问题的真解$u_0$的精确度, 目标是找一个逼近解$u_{\tau}\in H^1(\Omega)$使得

\[\| u_0-u_{\tau}\| _{\mathcal{E}(\Omega)}\le\tau,\]

其中能量范数定义为

\[\| u\| _{\mathcal{E}(\Omega)}=\left(\int_{\Omega}A\nabla u\cdot\nabla u\mathrm{d}x\right)^{\frac{1}{2}}.\]

再来定义问题$(2.1)$的弱形式. 对于Dirichlet边界条件, 我们记

\[H_q^1(\Omega)=\lbrace u\in H^1(\Omega)\vert u=q(x)\text{ on }\partial\Omega\rbrace ,\]

并且如果$q=0$那么记$H_0^1(\Omega)=H_q^1(\Omega)$. Dirichlet问题的弱解$u_0\in H_q^1(\Omega)$满足

\[B(u_0,v)=F(v), \quad \forall v\in H_0^1(\Omega), \tag{2.4}\]

其中,

\[B(u,v)=\int_{\Omega}A(x)\nabla u\cdot\nabla v\mathrm{d}x, \quad F(v)=\int_{\Omega}fv\mathrm{d}x.\]

而Neumann问题的弱解$u_0\in H^1(\Omega)$满足$(2.4)$, 其中

\[F(v)=\int_{\Omega}fv\mathrm{d}x+\int_{\partial\Omega}gv\mathrm{d}s, \quad \forall v\in H^1(\Omega).\]

于是, 能量范数也可以写成$| u| _{\mathcal{E}(\Omega)}=(B(u,u))^{\frac{1}{2}}.$

$\S 2.2$ 最佳逼近空间

下面考虑在问题$(2.1)$中让$f=0$, 并采用Neumann边界条件$(2.2)$, 真解设为$u_0$. 假设$\omega_i$是固定边长的($d$维)小正方体, 并且它被一个更大的正方体$\omega_i^\ast $围住. 我们需要探究$\omega_i\in\mathrm{int}(\Omega)$以及$\overline{\omega_i}\cap\Omega\ne\varnothing$两种情形.

为方便起见, 我们去掉下标.

$\S 2.2.1$ $\omega\in\mathrm{int}(\Omega)$的情形

考虑中心在原点的小正方体$\omega\subset\omega^\ast$, 边长分别为$\sigma$与$\sigma^\ast=(1+\rho)\sigma$.

首先我们考虑$\omega\in\mathrm{int}(\Omega)$的情形, 满足$\omega\subset\omega^\ast\subset\Omega$. 定义能量内积为

\[\begin{aligned} &(u,v)_{\mathcal{E}(\omega)}=\int_{\omega}A\nabla u\cdot\nabla v\mathrm{d}x, \\ &(u,v)_{\mathcal{E}(\omega^\ast )}=\int_{\omega^\ast}A\nabla u\cdot\nabla v\mathrm{d}x. \end{aligned}\]

我们要用$\omega^\ast $来构造$\omega$上的有限维逼近空间. 对$\Omega$中任意开的子集$S$, 我们定义函数空间$H_A(S)$由$H^1(S)$中满足A-harmonic的函数构成, 即$v\in H^1(\Omega)$并且

\[B(v,\varphi)=0, \qquad \forall \varphi\in C_0^{\infty}(\Omega).\]

这里, $H_A(\omega)$与$H_A(\omega^\ast )$包含了非均匀(heterogeneity)的局部信息, 所以可以用来构造最优的局部基函数.

我们记$H_A(\omega^\ast )/\mathbb{R}$表示$H_A(\omega^\ast )$关于常值函数的商空间(因为Neumann边界条件允许最终的解差一个常数), 于是$u_0$位于这个局部空间模掉常函数.

下面, 我们考虑逼近函数空间$H_A(\omega^\ast )/\mathbb{R}$(限制在$\omega$上). 我们取两个集合$\omega\subset\omega^\ast $是因为有Caccippoli不等式, 它可以用$u$在$\omega^\ast $上的$L^2$范数来控制$u$在$\omega$中的能量范数.

定理2.2.1(Cacciappoli不等式) 设$\mathcal{O}\subset\omega^\ast $是可测子集并且$\mathrm{dist}(\partial\mathcal{O},\partial\omega^\ast )>\delta>0$, $u$是$\omega^\ast $中的A-harmonic函数, 并且$u\in L^2(\omega^\ast )\cap H_{loc}^1(\omega^\ast )$, 则
\[\| u\| _{\mathcal{E}(\mathcal{O})}\le (2\beta^{\frac{1}{2}}\delta^{-1})\| u\| _{L^2(\omega^\ast )}.\]
其中$\beta$在椭圆算子的定义中出现.

记$P:H_A(\omega^\ast )/\mathbb{R}\to H_A(\omega)$表示限制算子, 满足

\[P(u)(x)=u(x), \quad \forall x\in\omega, \forall u\in H_A(\omega^\ast )/\mathbb{R}.\]

根据Cacciappoli不等式可知$P$是紧算子.

下面我们要用“$n$”维子空间$S(n)$(不是真正意义上的$n$维)来逼近$H_A(\omega^\ast )$. 为了定义局部逼近的精度, 我们引入度量

\[d(S(n),\omega)=\sup\limits_{u\in H_A(\omega^\ast )/\mathbb{R}} \inf\limits_{\chi\in S(n)}\dfrac{\| Pu-\chi\| _{\mathcal{E}(\omega)}}{\| u\| _{\mathcal{E}(\omega^\ast )}}.\]

称一列逼近空间$\hat{S}(n)$是最优的, 若它满足对任意的$n$维子空间$S(n)$都有

\[d(\hat{S}(n),\omega)\le d(S(n),\omega), \quad n=1,2,\cdots\]

我们找一列最优逼近空间的问题具体可如下表述：令

\[d_n(\omega,\omega^\ast )=\inf\limits_{S(n)}d(S(n),\omega^\ast ),\]

需要找$\lbrace \Psi_n(\omega)\rbrace _{n=1}^{\infty}$, 使得

\[d_n(\omega,\omega^\ast )=d(\Psi_n(\omega),\omega^\ast ).\]

我们把$d_n(\omega,\omega^\ast )$称为关于紧算子$P$的Kolmogorov $n$-width.

GFEM的最优局部逼近空间$\Psi_n(\omega)$可以具体表示出来. 我们引入伴随算子$P^\ast :H_A(\omega)\to H_A(\omega^\ast )/\mathbb{R}$，那么算子$P^\ast P:H_A(\omega^\ast )/\mathbb{R}\to H_A(\omega^\ast )/\mathbb{R}$是紧、自伴、非负的算子. 我们考虑下面问题的特征值和特征函数:

\[P^\ast Pu=\lambda u \tag{2.5}\]

分别把特征值和特征函数记为$\lbrace \varphi_i\rbrace $和$\lbrace \lambda_i\rbrace $.

定理2.2.2 最优逼近空间可以如下给出：$\Psi_n(\omega)=\mathrm{span}\lbrace \psi_1,\cdots,\psi_n\rbrace $, 其中$\psi_i=P\varphi_i$, $d_n(\omega,\omega^\ast )=\sqrt{\lambda_{n+1}}$.

定理2.2.3 最优逼近空间可以如下给出：$\Psi_n(\omega)=\mathrm{span}\lbrace \psi_1,\cdots,\psi_n\rbrace $, 其中$\psi_i=P\varphi_i$, 并且$\varphi_i$和$\lambda_i$是前$n$个特征函数和特征值, 满足
\[(\varphi_i,\delta)_{\mathcal{E}(\omega)}=\lambda_i(\varphi_i,\delta)_{\mathcal{E}(\omega^\ast )}, \forall \delta\in H_A(\omega^\ast )/\mathbb{R}. \tag{2.6}\]

下面的定理给出了最优局部逼近的收敛阶上界.

定理2.2.4 对于$\varepsilon>0$, 存在$N_{\varepsilon}>0$, 使得对任意$n>N_{\varepsilon}$有 $d_n(\omega,\omega^\ast )\le e^{-n^{\frac{1}{d+1}-\varepsilon}}.$

这个定理表明, 对于$\mathfrak{C}$中的所有$L^{\infty}(\Omega)$系数, 最优逼近空间关于$n$的渐近收敛阶都是几乎指数增长的.

$\S 2.2.2$ $\overline{\omega_i}\cap\Omega\ne\varnothing$的情形

假设有两个正方体$C,\omega^\ast $, 其中$C\subset\omega^\ast $并且边长分别为$\sigma$和$\sigma^\ast $. 我们假设$C$与$\partial\Omega$相交, 并且截取出来的区域记为$\omega= C\cap\Omega$, 如图所示.

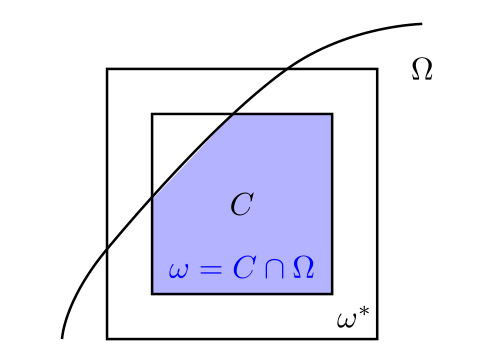
我们设$\partial\Omega$是$C^1$的（即边界可以用一个$C^1$函数的图像表示）.

对于Neumann问题, 给定函数$u\in H_A(\Omega)$, 我们需要给出在$\omega$中的局部逼近. 我们取一个局部的A-harmonic的特解$u_p$满足

\[n\cdot A\nabla u_p=g, \text{ on }\omega^\ast \cap\partial\Omega, \text{ 且}n\cdot A\nabla u_p=K_1\text{ on }\partial\omega^\ast \cap\Omega.\]

其中, 常数$K_1$满足可解性条件, $n$是边界$\omega^\ast \cap\Omega$的单位外法向量. 记$u=u_p+u_1$, 则

\[n\cdot A\nabla u_1=0 \text{ on }\omega^\ast \cap\partial\Omega \text{, 且}n\cdot A\nabla u_1=n\cdot A\nabla u-K_2\text{ on }\partial\omega^\ast \cap\Omega.\]

这里$K_2$合适选取使得满足可解条件.

对于Dirichlet问题, 那么我们假设特解$u_p$满足A-harmonic并且

\[u_p=q=u\text{ on }\omega^\ast \cap\partial\Omega, \text{ and }n\cdot A\nabla u_p=0\text{ on }\partial\omega^\ast \cap\Omega.\]

我们需要找一列最优局部逼近空间, 并且给出$u_0=u-u_p$在能量范数意义下的最佳逼近. 我们引入函数空间$H_{A,0}(\Omega\cap\omega^\ast )$表示所有$v\in H^1(\Omega\cap\omega^\ast )$满足在$\Omega\cap\omega^\ast $上是A-harmonic, 并且

\[n\cdot A\nabla v=0\text{ on }\partial\Omega\cap\omega^\ast .\]

类似我们定义空间$H_{A,0}(\omega)$. 由于我们在能量范数意义下逼近函数, 所以我们引入商空间$H_{A,0}(\Omega\cap\omega^\ast )/\mathbb{R}$.

定义$P:H_{A,0}(\omega^\ast \cap\Omega)/\mathbb{R}\to H_{A,0}(\omega)$表示限制算子, 定义为

\[P(u)(x)=u(x), \qquad \forall x\in\omega, \forall u\in H_{A,0}(\omega^\ast \cap\Omega)/\mathbb{R}.\]

可以证明$P$是紧算子.

设$S(n)$是$H_{A,0}(\omega)$的有限维子空间, 那么求最优局部逼近空间的问题可以用$P$的$n$-width来表示. 假设

\[d_n(\omega,\omega^\ast \cap\Omega)=\inf\limits_{S(n)}\sup\limits_{u\in H_{A,0}(\omega^\ast \cap\Omega)/\mathbb{R}} \inf\limits_{\chi\in S(n)}\dfrac{\| Pu-\chi\| _{\mathcal{E}(\omega)}}{\| u\| _{\mathcal{E}(\omega^\ast \cap\Omega)}}.\]

那么最佳逼近空间$\lbrace \Psi_n(\omega)\rbrace _{n=1}^{\infty}$满足

\[d_n(\omega,\omega^\ast \cap\Omega)=\sup\limits_{u\in H_{A,0}(\omega^\ast \cap\Omega)/\mathbb{R}} \inf\limits_{\chi\in \Psi_n(\omega)}\dfrac{\| Pu-\chi\| _{\mathcal{E}(\omega)}}{\| u\| _{\mathcal{E}(\omega^\ast \cap\Omega)}}.\]

下面, 我们引入伴随算子$P^\ast :H_A(\omega)\to H_A(\omega^\ast \cap\Omega)/\mathbb{R}$, 那么算子$P^\ast P$是$H_{A,0}(\omega^\ast \cap\Omega)/\mathbb{R}$到自身的紧算子. 我们可以类似前面来证明

定理2.2.5 最优逼近空间可以如下给出：$\Psi_n(\omega)=\mathrm{span}\lbrace \psi_1,\cdots,\psi_n\rbrace $, 其中$\psi_i=P\varphi_i$, 并且$\varphi_i\in H_{A,0}(\omega^\ast \cap\Omega)$和$\lambda_i$是前$n$个特征函数和特征值, 满足
\[(\varphi_i,\delta)_{\mathcal{E}(\omega)}=\lambda_i(\varphi_i,\delta)_{\mathcal{E}(\omega^\ast \cap\Omega)}, \forall \delta\in H_{A,0}(\omega^\ast \cap\Omega)/\mathbb{R}. \tag{2.7}\]

可以证明误差界估计:

定理2.2.6 对$\varepsilon>0$, 存在$N_{\varepsilon}>0$使得对任意$n>N$,
\[d_n(\omega,\omega^\ast \cap\Omega)\le e^{-n^{\frac{1}{d+1}-\varepsilon}}.\]

定理表明, 对于$\mathfrak{C}$中的所有$L^{\infty}(\Omega)$系数, 在边界附近的最优逼近空间关于$n$的渐近收敛阶也是几乎指数增长的.

$\S 2.2.3$ 放在一起

下面我们要把前面的定理2.2.4和定理2.2.6合在一起. 给定$\Omega$的划分$\omega_i, i=1\cdots m$, 记在$\omega_i$上的子空间为$\hat{\Psi}_i(i=1:m)$, 我们把常函数加上去然后记$\Psi_i=\hat{\Psi}_i\oplus\mathbb{R}$.

如果区域$\omega_i\cap\partial\Omega\ne\varnothing$, 那么我们取局部逼近函数空间为$\Psi_i\oplus u_p^i$, 其中$u_p^i\in H_A(\omega_i^\ast \cap\Omega)$是前一节引入的特解. 记$\dim \Psi_i=N_i$, $N=m\times\sum_{i=1}^mN_i$.

根据这里的定理2、定理2.2.4和定理2.2.6, 我们有

定理2.2.7(GFEM的几乎指数逼近) 对$\varepsilon>0$, 存在$N_{\varepsilon}>0$使得对任意$N>N_{\varepsilon}$, 对于$\omega_i\cap\partial\Omega=\varnothing$, 存在$\zeta_i\in\Psi_i$; 而对于$\omega_i\cap\partial\Omega\ne\varnothing$, 存在$\zeta_i\in\Psi_i\oplus u_p^i$. 并且存在常数$K$(与$N$无关)使得如下给出的$\zeta\in H^1(\Omega)$:
\[\zeta(x)=\sum_{i=1}^m\zeta_i(x)\phi_i(x)\]
满足
\[\| u_0-\zeta\| _{L^2(\Omega)}\le Ke^{-N^{\frac{1}{1+d}-\varepsilon}}\]
和
\[\| u_0-\zeta\| _{\mathcal{E}(\Omega)}\le Ke^{-N^{\frac{1}{1+d}-\varepsilon}}.\]

$\S 2.3$ GFEM方法的具体实现

在构造局部逼近空间的时候, 每个空间之间的函数都是线性无关的, 所以可以很好地并行化. 而这也是GFEM的高效之处. 局部逼近空间的基函数(shape functions)的一个有效选取方式是可以用问题$(2.6)$和$(2.7)$的特征函数. 这个方式是基于Rayleigh-Ritz逼近的. 另外, 由于我们建立了几乎指数阶收敛的结果, 所以实际上并不需要太多特征函数就能有比较好的逼近效果.

下面的讨论中我们省略下标$i$, 并假设$\omega_i$都有相同的大小.

GFEM方法的具体实现过程如下:

a. 给定$\omega^\ast $和$\Psi$的维数$N$, 我们构造$M>N$个定义在$\partial\omega^\ast $上的函数$\varsigma_k$, $k=1,2,\cdots$. 当$M$趋于无穷的时候, 应该要得到一个稠密子集.

我们可以发现, $\varsigma_k$的最佳取法是满足Laplace方程的$k$次调和多项式的迹(trace), 以及其他满足常系数椭圆方程$\mathrm{div}(A\nabla u)=0$的多项式. 利用这些函数, 我们可以用数值方法求出$\omega^\ast $上由A-harmonic函数$u_{\varsigma_k}$(满足Neumann边界条件 $n\cdot A\nabla u=\varsigma_k$)构成的$M$维空间$\mathfrak{S}$(花体$S$). 我们要用$\mathfrak{S}$来构造我们想要的$N$个特征值和特征函数, 然后这些特征函数构成GFEM的局部逼近空间$\Psi$. 而$M$和$N$的选取是由前面的误差界决定的.

对于每个区域$\omega_i$, 上述构造过程可以并行化. 我们用这些结论来构造局部刚度矩阵, 然后用单位分解函数把这些局部基函数拼成总刚度矩阵和右端向量. 而拼接的步骤也是可以并行化进行的.

b. 求解总刚度矩阵和右端向量对应的方程组.

c. 计算我们关心的局部信息, 例如纤维在边界处的压力.

下面我们简单估计一下每一步的计算量.

a. 我们用有限元网格覆盖$\omega^\ast $, 网格大小为$h$, 然后求解$\mathrm{div}(A\nabla u)=0$ (其中Neumann边界条件$n\cdot A\nabla u=\varsigma_k$). 这样我们得到A-harmonic函数$u_{\varsigma}^h$.

如果用Gauss消去法(LU分解), 那么我们就需要$(\vert \omega^\ast \vert h^{-2})^{-2}$次运算(刚度矩阵是稀疏的), 由于$M\ll h^{-2}$, 所以计算$M$个函数不会改变运算次数的阶. 另外, 计算$N$个特征函数的计算量也很小, 于是构造$\Psi$所需的计算量的阶是$\vert \omega_i\vert ^{-2}h^{-4}$. 计算刚度矩阵的每个分量不会改变阶. 所以主要的问题在于选取合适的网格尺寸$h$使得我们能达到一个合适的精度.

如果边界函数$\varsigma_k$是光滑的, 例如前面提到的调和多项式的迹, 那么我们猜测(还没证明)精度为

\[\varepsilon_{\varsigma i}=\| u_{\varsigma i}-u_{\varsigma i}^h\| _{\mathcal{E}(\omega)} \le Ch^{\gamma}M^{\delta}\| u\| _{\mathcal{E}(\omega^\ast )}.\]

如果$M$比较小, 那么$M$带来的影响可以忽略. 利用这些函数我们可以构造逼近空间$\Psi^h$, 然后这些逼近空间可以用来构造GFEM格式.

b. 对总刚度矩阵用Gauss消去法, 我们可以得到$\Omega$上的一个逼近解. 在子区域$\omega$上, 用逼近空间$\Psi^h$(代替$\Psi$)来逼近真解$u$的误差阶是$Ce^{-N^{\frac{1}{1+d}-\varepsilon}}$. 总刚度矩阵的大小是$N\vert \Omega\vert /\vert \omega\vert $. 由于总刚度矩阵是稀疏的, 所以用消去法来求解线性方程组所需计算量是 $(N\times \vert \Omega\vert /\vert \omega\vert )^{-4}$. 所以我们还要思考如何选取合适的$\omega$的大小.

前面我们考虑的都是$f=0$的情形, 而如果$f\ne 0$, 那么我们引入问题$(2.1)$在$\omega_i^\ast $上的局部特解, 其中在$\partial\omega_i^\ast $上有常数的Neumann边界条件(这个常数的选取需要满足相容性条件). 这个问题并不难求解, 因为刚度矩阵已经拼接出来了. 我们把局部特解记为$u_{\omega_i}$, 然后在每个$\omega_i$上, 我们采取的逼近空间是

\[\Psi_i=\hat{\Psi}_i \oplus u_{\omega_i}.\]

$\S 2.3.1$ 混合边界条件情形的具体解法

最后再来看看[Babuska et al., 2019]中用Multiscale-Spectral GFEM(MS-GFEM)算法的步骤.

我们的问题是求解

\[-\mathrm{div}(A(x)\nabla u(x))=f(x), \qquad x\in\Omega\subset\mathbb{R}^2,\]

其中Neumann边界条件定义在$\partial\Omega_N\subset\partial\Omega$, 满足

\[n\cdot A(x)\nabla u(x)=g(x), \quad x\in\partial\Omega_N,\]

并且Dirichlet边界条件定义在$\partial\Omega\subset\partial\Omega$, 满足

\[u=h, \qquad x\in\partial\Omega_D.\]

这里, $\partial\Omega_D\cap\partial\Omega_N=\varnothing$, 并且$\overline{\partial\Omega_D}\cup\overline{\partial\Omega_N}=\partial\Omega.$

上述问题的弱解位于

\[H_D^1(\Omega)=\lbrace u\in H^1(\Omega):u=h\text{ on }\partial\Omega_D\rbrace .\]

上述问题的弱形式为

\[B(u,v)=F(v), \forall v\in H_{0D}^1=\lbrace v\in H^1(\Omega):v=0\text{ on }\partial\Omega_D\rbrace \tag{2.8}\]

其中,

\[B(u,v)=\int_{\Omega}A(x)\nabla u\cdot\nabla v\mathrm{d}x, \quad F(v)=\int_{\Omega}fv\mathrm{d}x+\int_{\partial\Omega_N}gv\mathrm{d}x,\]

下面我们来看一下刻画MS-GFEM方法的局部最优逼近空间的构造方法. 局部最优逼近空间构造的主要思想是用over-sampling, 并且它由A-harmonic函数的限制算子$P$的一些特征函数张成. (A-harmonic函数$\xi$满足

\[-\mathrm{div}(A(x)\nabla \xi(x))=0\text{ on }\omega_i^\ast .\]

我们把这样的函数构成的空间记为$H_A(\omega_i^\ast )$).

为了构造局部基函数, 首先让$\lbrace \omega_i^\ast \rbrace _{i=1}^N$是另外一系列的开集, 满足$\omega_i\subset\omega_i^\ast $. 对于内部区域, 我们要求$\mathrm{dist}(\partial\omega_i^\ast ,\partial\omega_i)>0$. 对于边界区域(即满足$\partial\omega_i\cap\partial\Omega\ne\varnothing$的区域), 我们要求$\mathrm{dist}(\partial\omega_i^\ast \cap\Omega,\partial\omega_i\cap\Omega)>0$.

局部逼近函数是由一个特解和一个局部逼近空间$V_{\omega_i}^{m_i}$(通解)构成的. 而局部逼近空间的构造顺序是先构造$\omega_i^\ast $上的有限维空间$V_{\omega_i^\ast }^{m_i}$, 然后再把定义域限制在$\omega_i$上, 得到逼近空间$V_{\omega_i}^{m_i}$. 在MS-GFEM中, $V_{\omega_i}^{m_i}$是A-harmonic函数上的限制算子$P$的前几个特征值对应的特征函数张成的空间. 全局逼近空间定义为

\[V^N=\left\lbrace \sum_{i=1}^N\phi_i\xi_i:\xi_i\in V_{\omega_i}^{m_i}\right\rbrace ,\]

那么$V^N$是$H_{0D}^1(\Omega)$的子空间. 而边界条件以及原问题的右端项是通过求特解来处理的. 这里, 局部特解$\chi_i\in H^1(\omega_i^\ast )$满足

\[-\mathrm{div}(A(x)\nabla\chi_i(x))=f(x), \qquad x\in\omega_i^\ast .\]

在内部区域中我们假设$\chi_i=0$在$\partial\omega_i^\ast $上成立. 而在边界区域中, 我们假设$\chi_i$在$\partial\omega_i^\ast \cap\partial\Omega$上满足Neumann边界条件或者Dirichlet条件, 而在$\partial\omega_i^\ast \cap\Omega$上满足$\chi_i=0$. 计算完局部特解之后可以构建全局特解$u^F$, 定义为

\[u^F=\sum_{i=1}^N\phi_i\chi_i.\]

这样, 问题$(2.8)$的MS-GFEM逼近解可以写成$u_0=u^G+u^F$, 其中

\[u^G\in V^N=\left\lbrace \sum_{i=1}^N\phi_i\xi_i:\xi_i\in V_{\omega_i}^{m_i}\right\rbrace ,\]

下面我们陈述具体的应用步骤.

实际上, 我们最终目的是在$V^N$中找一个逼近解, 即
\[u^G=\sum\limits_{i=1}^Nc_i\phi_i\xi_i, \qquad \xi_i\in V_{\omega_i}^{m_i},\]
而$\phi_i$是已经预先给定的, 所以我们需要想办法求局部的逼近解$\xi_i$. 而在MS-GFEM中, 为了求局部逼近解$\xi_i\in V_{\omega_i}^{m_i}$, 需要用到有限元方法. 而传统的有限元方法需要打网格, 所以我们就在$\Omega$上打一个网格, 那么局部解就用有限元函数来逼近, 比如用二次函数来近似$V_{\omega_i}^{m_i}$中的函数. 而这就要构建一个局部逼近解空间$S_{\omega_i}^{m_i}$.

我们要在整个区域$\Omega$上用标准有限元网格作剖分. 未来工作中我们再在每个$\omega_i$上用独立的网格, 充分利用局部计算的并行性质. MS-GFEM的步骤为:

1. 定义$\Omega$的剖分为正方形子区域$\lbrace \omega_i\rbrace _{i=1}^N$, 并延展到$\lbrace \omega_i^\ast \rbrace _{i=1}^N$, 使得$\omega_i\subset\omega_i^\ast $中心相同且$\omega_i$和$\omega_i^\ast $边长的比值小于1.

2. 构造$\lbrace \omega_i\rbrace _{i=1}^N$上的单位分解函数$\lbrace \phi_i\rbrace _{i=1}^N$. 我们用定义在三角形和正方形的标准的双线性二次型函数(shape function)来构造单位分解函数.

3. 求解局部特解$\lbrace \chi_i\rbrace _{i=1}^N$满足

\[-\mathrm{div}(A(x)\nabla\chi_i(x))=f(x), \qquad x\in\omega_i^\ast .\]

4. 构造

\[B(u^G,v)=F(v)-B(u^F,v)\]

的右端向量记为$\boldsymbol{r}$.

5. 构造有限维局部空间$S_{\omega_i^\ast }^{n_i}\subset H_A(\omega_i^\ast )$. 这里$S_{\omega_i^\ast }^{n_i}$可以看做$H_A(\omega_i^\ast )$的离散逼近. 这些有限维空间的维数是$n_i$, 并且里面的元素是边界信息的A-harmonic延拓 (用$\partial\omega_i^\ast $上分片线性的hat function来表示). 这些分片线性函数可以构成$\partial\omega_i^\ast $的单位分解.

6. 求解$S_{\omega_i^\ast }^{n_i}$的local spectral problems, 得到一个local spectral bases, 它可以张成$V_{\omega_i}^{m_i}$(其中$n_i>m_i$).

7. 构造

\[B(u^G,v)=F(v)-B(u^F,v)\]

的总刚度矩阵$\boldsymbol{G}$, 其分量为$B(u,v)$, 其中$u,v\in V^N$.

8. 求解$\boldsymbol{Gx}=\boldsymbol{r}$.

9. 逼近解可以如下给出: $u_0=u^G+u^F$.

$\S 2.3.2$ $S_{\omega_i^\ast }^{n_i}$的构造

假设$\Omega=\bigcup\limits_{i=1}^N\omega_i$, 并且有$\omega_i\subset\omega_i^\ast $. 记$\mathcal{H}=\lbrace E_e\rbrace_{e=1}^{n_{el}}$是$\Omega$的有限元网格, %而每个$E_e$它们与$\partial\omega_i$和$\partial\omega_i^\ast $协调(conform), $i=1,\cdots,N$. 把双线性、二次的型函数记为$H_n(\alpha)$, 其中$\alpha=(\alpha_1,\alpha_2)$是reference element (如: 顶点在$(0,0),(1,0),(0,1),(1,1)$的单位正方形)的坐标, $x=(x_1,x_2)$是$\Omega$的笛卡尔坐标. 映射$\alpha_e:E_e\to \square$把第$e$个有限元$E_e$映为reference element $\square$.

我们生成$S_{\omega_i^\ast }^{n_i}$为下面问题的A-harmonic有限元解:

\[\left\lbrace \begin{aligned} &-\mathrm{div}(A(x)\nabla w_i^k(x))=0, && x\in\omega_i^\ast , \\ &w_i^k(x)=h_i^k(x), && x\in\partial\omega_i^\ast , \end{aligned}\right.\]

其中$h_i^k(x)$是第$k$个hat function, 定义为在$\partial\omega_i^\ast \cap\Omega$的第$k$个边界结点上满足$h_i^k=1$, 而在其他结点满足$h_i^k=0$, 这里$1\le k\le n_i$.

在边界的子区域, $\partial\omega_i^\ast \cap\partial\Omega\ne\varnothing$. 只在内部结点$\partial\omega_i^\ast \cap\Omega$对应的hat function用作边界条件, 而$h_i^k(x)$在$\partial\omega_i^\ast \cap\partial\Omega_N$满足Neumann条件, 在$\partial\omega_i^\ast \cap\partial\Omega_D$满足Dirichlet条件. 我们把$\omega_i^\ast $上的第$k$个A-harmonic函数记为

\[w_i^k(x)=\sum_{e=1}^{N_{el}}\sum_{l=1}^{n_{en}}w_{i,e}^{k,l}H_l(\alpha_e(x)), \tag{2.9}\]

其中

$\mathbf{w}^k_{i,e}$ 是$E_e$中结点处的值构成的向量$(1\le e\le n_{el})$,
$w_{i,e}^{k,l} $ 是$\mathbf{w}^k_{i,e}$在第$l$个结点对应的分量, $1\le l\le n_{en}$.

$\S 2.3.3$ 局部Spectral Bases $V_{\omega_i}^{m_i}$的构造

下面构造spectral basis, 在局部逼近空间上得到最优逼近性质. 引入$V_{\omega_i^\ast }^{m_i}=\mathrm{span}\lbrace \xi_i^1,\cdots,\xi_i^{m_i}\rbrace $, 其中$\xi_i^j$是下面问题从大到小排列的第$j$个特征值:

\[Q_i\boldsymbol{x}=\lambda P_i\boldsymbol{x},\]

其中, $Q_i,P_i$的各个分量是

\[\begin{aligned} Q_i^{jk}&=(w_i^j,w_i^k)_{\mathcal{E}(\omega_i)}=\int_{\omega_i}A\nabla w_i^j\cdot \nabla w_i^k\mathrm{d}x =\int_{\partial\omega_i}(n\cdot A\nabla w_i^j)w_i^k\mathrm{d}s, \\ P_i^{jk}&=(w_i^j,w_i^k)_{\mathcal{E}(\omega_i^\ast )}=\int_{\omega_i}A\nabla w_i^j\cdot \nabla w_i^k\mathrm{d}x =\int_{\partial\omega_i^\ast }(n\cdot A\nabla w_i^j)w_i^k\mathrm{d}s, \end{aligned}\]

在局部区域, 我们用$S_{\omega_i^\ast }^{n_i}$中得到的基函数$w_i^k(x)$来逼近$H_A(\omega_i^\ast )$, 然后我们考虑$V_{\omega_i}^{m_i}=\mathrm{span}\lbrace \xi_i^1,\cdots,\xi_i^{m_i}\rbrace $得到$\omega_i$上的离散逼近. 向量$\boldsymbol{x}$的第$k$个分量就是第$k$个基函数$w_i^k(x)\in S_{\omega_i}^{n_i}$的系数, 所以$\omega_i^\ast $上第$q$个特征函数$(1\le q\le m_i)$如下给出:

\[\xi_i^q(x)=\sum_{k=1}^{m_i}\xi_i^{q,k}w_i^k(x), \tag{2.10}\]

其中$x_k=\xi_i^{q,k}$是系数. 这样, 我们可以得到特征函数

\[\lbrace \xi_i^1,\xi_i^2,\cdots,\xi_i^{m_i}\rbrace ,\]

其中对应的特征值是$1>\lambda_i^1\ge \lambda_i^2\ge\cdots\ge\lambda_i^{m_i}>0$. (注意$P_i,Q_i$是对称正定的)

于是, 结合$(2.9)$和$(2.10)$可知$n$-width特征函数可以有如下的有限元逼近:

\[\xi_i^q(x)=\sum_{e=1}^{n_{el}}\sum_{k=1}^{m_i}\sum_{i=1}^{n_{en}} \xi_i^{q,k}w_{i,e}^{k,l}H_l(\alpha_e(x)).\]

$\S 2.3.4$ 拼装总刚度矩阵与右端向量

利用$V_{\omega_i}^{m_i}$中的基函数, 我们可以把它们拼成全局的函数空间

\[V^n=\mathrm{span}\lbrace \phi_i\xi_i^q:1\le i\le N, 1\le q\le m_i, \xi_i^q\in V_{\omega_i}^{m_i}\rbrace .\]

而Galerkin离散

\[B(u^G,v)=F(v)-B(u^F,v)\]

可以写成一个线性方程组$G\boldsymbol{x}=\boldsymbol{r}$, 其中, 矩阵$G$的分量为

\[G_{iqjr}=(\phi_i\xi_i^q,\phi_j\xi_j^r)_{\mathcal{E}(\Omega)}.\]

$G$的第$ij$块对应函数$\phi_iV_{\omega_i}^{m_i}$和$\phi_jV_{\omega_j}^{m_j}$的cross products, 而$\boldsymbol{x}$的第$iq$个分量是$\phi_i\xi_i^q$的系数. 这样, 通过求解这个线性方程组, 我们就能得到

\[u^G=\sum_{i=1}^N\sum_{q=1}^{m_i}x_i^q\phi_i\xi_i^q,\]

类似地, 右端向量的各个分量是

\[\boldsymbol{r}_{iq}=F(\phi_i\xi_i^q)-B(u^F,\phi_i\xi_i^q) =\int_{\Omega}f\phi_i\xi_i^q\mathrm{d}x +\int_{\partial\Omega_N}g\phi_i\xi_i^q\mathrm{d}S -\int_{\Omega}u^F\phi_i\xi_i^q\mathrm{d}x.\]

最终我们可以得到逼近解为

\[u_0=u^G+u^F=\sum_{i=1}^N\sum_{q=1}^{m_i}x_i^q\phi_i\xi_i^q+\sum_{i=1}^N\phi_i\chi_i.\]