发布日期:2022年9月22日
GFEM overview
目录
考虑下面的问题, 其中$\Omega\subset\mathbb{R}^2$, $\Gamma=\partial\Omega:=\Gamma_1\cup\Gamma_2$, 并且
\[\left\lbrace \begin{aligned} &-\mathrm{div}(a(x,y)\nabla u)=f, &&(x,y)\in\Omega, \\ &u=0, &&\text{ on } \Gamma_1, \\ &a\dfrac{\partial u}{\partial n}=g, &&\text{ on }\Gamma_2. \end{aligned}\right. \tag{1}\]记
\[\begin{gathered} \|v\|_{\mathcal{E}(\Omega)}^2:=\int_{\Omega}a|\nabla v|^2\mathrm{d}x, \\ \|v\|_{L_a^2(\Omega)}^2:=\int_{\Omega}a|v|^2\mathrm{d}x, \\ \mathcal{E}(\Omega):=\left\lbrace v: \|v\|_{\mathcal{E}(\Omega)}^2 < \infty\right\rbrace \\ \mathcal{E}_{\Gamma_1}(\Omega):=\lbrace v:v\in\mathcal{E}(\Omega), u=0\text{ on }\Gamma_1\rbrace . \end{gathered}\]1 构造广义有限元方法框架要实现的目标
- 构造有限元空间$S$使得$S\subset\mathcal{E}_{\Gamma_1}(\Omega)$;
- 存在$\xi=\xi^u\in S$使得$|u-\xi^u|_{\mathcal{E}(\Omega)}$很小.
2 广义有限元方法的基本要素
(1)一族集合$\lbrace \omega_j\rbrace _{j=1}^N$使得它们可以覆盖边值问题的区域$\Omega$.
我们假设$\lbrace \omega_j\rbrace _{j=1}^N$满足如下条件:
- $\omega_j\subset\Omega\text{并且}\Omega=\bigcup_{j=1}^N\omega_j.$
- 任意$x\in\Omega$至多属于$\kappa$个子区域$\omega_j$.
(2)一族定义在$\Omega$上的函数$\lbrace \phi_j\rbrace _{j=1}^N$, 有分片连续的一阶导数并且满足:
- (2.1):$\phi_j(x,y)=0, \forall (x,y)\in\Omega\setminus\omega_j$, $j=1,\cdots,N$;
- (2.2):单位分解(Partition of unity): $\sum\limits_{j=1}^N\phi_j(x,y)=1$, $\forall (x,y)\in\Omega$;
- (2.3):$\max\limits_{(x,y)\in\Omega}\vert\phi_j(x,y)\vert\le C_1$, $j=1,\cdots N$;
- (2,4):$\max\limits_{(x,y)\in\Omega}\vert\nabla\phi_j(x,y)\vert\le\dfrac{C_2}{\mathrm{diam}(\omega_j)}$, $j=1,\cdots,N$;
(3)逼近的原理.
对于$\lbrace \omega_j\rbrace $中的任意一个$\omega_j$, 我们定义一个$m(j)$-维函数空间, 称为局部逼近空间(local approximation space):
\[V_j=\lbrace \xi_j:\xi_j=\sum_{i=1}^{m(j)}b_{ji}\xi_{ji}, b_{ji}\in\mathbb{R}, \xi_{ji}\in\mathcal{E}(\omega_j), \text{ and }\xi_{ji}=0\text{ on }\overline{\omega}_j\cap\Gamma_1\rbrace .\]然后, 令
\[\begin{aligned} S^{GFEM}&=\left\lbrace \psi=\sum_{j=1}^N\phi_j\xi_j: \xi_j\in V_j\right\rbrace \\ &=\mathrm{span}\lbrace \eta_{ji}, i=1,\cdots,m(j); j=1,\cdots,N\rbrace . \end{aligned}\]其中
\[\eta_{ji}=\phi_j\xi_{ji}\]是$S^{GFEM}$的形函数(shape functions). 把$S^{GFEM}$叫做广义有限元的全局逼近空间(global approximation space).
定理1: $S^{GFEM}\subset\mathcal{E}_{\Gamma_1}(\Omega).$
对任意$j$, 我们假设问题$(1)$的精确解$u\in \mathcal{E}_{\Gamma_1}$在$\omega_j$上可以被函数$\xi_j^u\in V_j$来逼近, 具体来说,
\[\begin{gathered} \|u-\xi_j^u\|_{L_a^2(\omega_j)}^2=\int_{\omega_j}a|u-\xi_j^u|^2\mathrm{d}x\mathrm{d}y\le\varepsilon_1^2(j); \\ \|u-\xi_j^u\|_{\mathcal{E}(\omega_j)}^2=\int_{\omega_j}a|\nabla(u-\xi_j^u)|^2\mathrm{d}x\mathrm{d}y\le\varepsilon_2^2(j). \end{gathered}\]然后我们定义全局逼近函数如下:
\[\xi^u=\sum_{j=1}^N\phi_j\xi_j^u\in S^{GFEM}.\]定理2 设$u\in\mathcal{E}_{\Gamma_1}(\Omega)$. 则
\[\|u-\xi^u\|_{L_a^2(\Omega)}\le\kappa^{1/2}C_1\left(\sum_{j=1}^N\varepsilon_1^2(j)\right)^{1/2}\]并且
\[\|u-\xi^u\|_{\mathcal{E}(\Omega)}\le(2\kappa)^{1/2} \left(C_2^2\sum_{j=1}^N\dfrac{\varepsilon_1^2(j)}{\mathrm{diam}(\omega_j)^2}+C_1^2\sum_{j=1}^N\varepsilon_2^2(j)\right)^{1/2}.\]
现在我们希望$\varepsilon_2(j)$跟$\varepsilon_1(j)/\mathrm{diam}(\omega_j)$成比例, 这样上述估计就可以简化. 它的一个充分条件可以是施加类似于Poincare-Friedrichs不等式的条件.
定理3 设$u\in\mathcal{E}_{\Gamma_1}(\Omega)$, 且$\lbrace \omega_j\rbrace ,\lbrace V_j\rbrace $满足如下假设:
(a)对任意$j$, 其中
\[\overline{\omega}_j\cap\Gamma_1=\varnothing,\]$V_j$包含常值函数并且对任意$v\in\mathcal{E}(\omega_j)$满足$\int_{\omega_j}av\mathrm{d}x\mathrm{d}y=0$都有
\[\|v\|_{L_a^2(\omega_j)}\le C_3\mathrm{diam}(\omega_j)\|v\|_{\mathcal{E}(\omega_j)}\](b)对任意$j$, 其中
\[\vert\overline{\omega}_j\cap\Gamma_1\vert>0,\]对任意$v\in\mathcal{E}(\omega_j)$, 当
\[v\vert_{\overline{\omega}_j\cap\Gamma_1}=0\]时, 都有
\[\|v\|_{L_a^2(\omega_j)}\le C_4\mathrm{diam}(\omega_j)\|v\|_{\mathcal{E}(\omega_j)}.\]那么存在$\tilde{\xi}_j^U\in V_j$使得全局逼近函数
\[\tilde{\xi}^u=\sum_{j=1}^N\phi_j\tilde{\xi}_j^u\]满足
\[\begin{gathered} \|u-\tilde{\xi}^u\|_{L_a^2(\Omega)}\le C_5\left(\sum_{j=1}^N[\mathrm{diam}(\omega_j)]^2\varepsilon_2^2(j)\right)^{1/2}, \\ \|u-\tilde{\xi}^u\|_{\mathcal{E}(\Omega)}\le C_6\left(\sum_{j=1}^N\varepsilon_2^2(j)\right)^{1/2}. \end{gathered}\]其中$C_5=\sqrt{\kappa}C_1(C_3^2+C_4^2)^{1/2}$并且$C_6=\lbrace 2\kappa(C_1^2+C_2^2(C_3^2+C_4^2))\rbrace ^{1/2}.$
下面回到GFEM. 下设定理3的假设成立并且$u\in\mathcal{E}_{\Gamma_1}$是下面问题的解:
\[B(u,v)=F(v), \forall v\in\mathcal{E}_{\Gamma_1}.\]则根据定理3的假设(b),
\[\|u-u_{GFEM}\|_{\mathcal{E}(\Omega)}\le C\|u-\tilde{\xi}_j^u\|_{\mathcal{E}(\Omega)} \le C\left(\sum \varepsilon_2^2(j)\right)^{1/2}.\]我们把上述估计写成下面的等价形式:
\[\|u-u_{GFEM}\|_{\mathcal{E}(\Omega)}\le C\inf\limits_{\xi_j^u\in V_j} \left(\sum \|u-\xi_j^u\|_{\mathcal{E}(\omega_j)}\right)^{1/2}.\]现在把$u^{GFEM}$写成
\[u_{GFEM}=\sum_{j=1}^N\sum_{i=1}^{m(j)}c_{ji}\eta_{ji},\]其中$\boldsymbol{c}=\lbrace c_{ji}\rbrace $是下述线性方程组的解:
\[\sum_{j=1}^N\sum_{i=1}^{m(j)}B(\eta_{lk},\eta_{ji})c_{ji}=F(\eta_{lk}), \qquad 1\le k\le m(l), 1\le l\le N.\]或者
\[A\boldsymbol{c}=\boldsymbol{F}.\]其中, $A$是刚度矩阵,其各个分量为
\[A(l,k; j,i)=B(\eta_{lk},\eta_{ji})=\int_{\omega_j\cap\omega_l}\nabla \eta_{lk}\cdot\nabla\eta_{ji}\mathrm{d}x.\]$\boldsymbol{F}$是右端向量, 其各个分量为
\[F(l;k)=\int_{\omega_l}f\eta_{lk}\mathrm{d}x+\int_{\Gamma_1\cap\bar{\omega}_l}g\eta_{lk}\mathrm{d}s.\]3 局部逼近空间$V_j$的选取
3.1 用$u$的信息
$V_j$的选取可以根据问题(1)精确解的一些性质来确定.
(a)用$u$所在Sobolev空间的信息来确定:
首先假设我们只知道$u\in H^m(\omega_j)$并且
\[\|u\|_{H^m(\omega_j)}=\left(\int_{\omega_j}\sum_{|k|\le m}(D^ku)^2\mathrm{d}x\right)^{1/2} \le K_j^{(m)}, m=0,1,\cdots; j=1,\cdots,N.\]希望选取空间$V_j$使得
\[\sup\limits_{\substack{u\in\mathcal{E}(\omega_j) \\ \|u\|_{H^m(\omega_j)}\le K_j^{(m)}}} \inf_{\xi_j\in V_j}\|u-\xi_j\|_{\mathcal{E}(\omega_j)} \text{很小}.\]那么定义在$\omega_j$上次数不超过$p$的多项式空间就适合作为$V_j$. 我们把它记为$W_j^{(p)}$, 则对$m\ge 1$, 有
\[\varepsilon_2(j)\le CK_j^{(m)}\dfrac{h_j^{\min(p,m-1)}}{p^{m-1}},\]其中$h_j=\mathrm{diam} \omega_j$.
(b)用$u$满足的边值问题信息来确定:
除了(a), 我们假设$u$满足边值问题$(1)$. 通常我们知道的信息更多, 例如如果$u$是问题$(1)$在$a=1$且$f=0$情形的解,即
\[\left\lbrace \begin{aligned} &-\Delta u=0, &&(x,y)\in\Omega, \\ &u=0, &&\text{ on } \Gamma_1, \\ &\dfrac{\partial u}{\partial n}=g, &&\text{ on }\Gamma_2. \end{aligned}\right. \tag{2}\]则$u$是调和函数. 这样, 我们可以用调和多项式(harmonic polynomials). 令
\[{^{\mathcal{H}}}W_j^{(p)}=\Big\lbrace v\in W_j^{(p)}: v\text{ is harmonic on }\omega_j\Big\rbrace .\]如果$\omega_j$是关于球的星形区域且边界$\partial\omega_j$是分片解析的, 其内角满足$\alpha_j=\beta_j\pi$, 其中$0\le \beta_j < 2-\lambda$, $\lambda>0$. 则对于${^{\mathcal{H}}}W_j^{(p)}$中的形函数, 可以证明
\[\varepsilon_2(j)\le CK_j^{(m)}h^{m-1}\left(\dfrac{\ln p}{p}\right)^{(2-\lambda)(m-1)}, \qquad p\ge m-1, m\ge 1,\]其中$K_j^{(m)}$在(a)中已经列出, 且$C$依赖于$\omega_j$的形状.
$\dim{^{\mathcal{H}}}W_j^{(p)}=2p+1$, $\dim W_j^{(p)}=\dfrac{(p+1)(p+2)}{2}$.
如果方程的右端项不是$0$, 那么我们就需要加一些额外的形函数,例如对于$f=1$, 我们添加形函数$\xi=x^2+y^2$.
3.2 当$\omega_j$形状复杂时$V_j$的选取
下面考虑问题$(2)$.
我们前面默认假设$\omega_j$是单连通区域. 现在我们假设$\omega_j$中间挖了个圆, 其中这个圆以某个点$(\bar{x},\bar{y})\in\Omega$为圆心.
假设
\[\Omega\supset\omega_j=\omega_j^{(1)}\setminus \omega_j^{(2)},\]其中
\[\begin{aligned} \omega_j^{(1)}&=\lbrace (x,y):|x-\bar{x}|<h, |y-\bar{y}|<h\rbrace , \\ \omega_j^{(2)}&=\lbrace (x,y):(x-\bar{x})^2+(y-\bar{y})^2<\delta^2, \text{ where }\delta<h\rbrace . \end{aligned}\]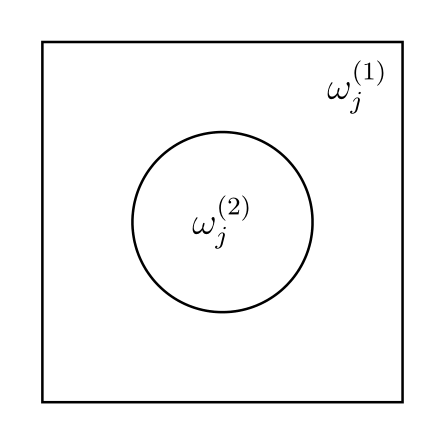
然后我们再假设$\partial\omega_j^{(2)}\subset\Gamma_2$并且在$\partial \omega_j^{(2)}$上满足$g=0$, 即在问题$(2)$中有$\dfrac{\partial u}{\partial n}=0$ on $\partial \omega_j^{(2)}$.
现在考虑函数
\[\begin{aligned} \xi_{j,l}^{(1)}(r,\theta)&=(r^l+r^{-l}\delta^{2l})\sin l\theta, \qquad l=1,2,\cdots \\ \xi_{j,l}^{(2)}(r,\theta)&=(r^l+r^{-l}\delta^{2l})\cos l\theta, \qquad l=0,1,2,\cdots, \end{aligned} \tag{3}\]其中$(r,\theta)$是以$(\bar{x},\bar{y})$为原点的极坐标.
命题4 $\xi_{j,l}^{(i)}, i=1,2$是调和函数并且满足 $\dfrac{\partial\xi_{j,l}^{(i)}}{\partial n}=0$ on $\partial\omega_j^{(2)}$.
由于$u$是$\omega_j$中的调和函数, 所以它可以关于$(3)$展开成洛朗级数:
\[u(r,\theta)=2a_0+\sum\limits_{l=1}^{\infty}a_l\xi_{j,l}^{(2)}(r,\theta) +\sum_{l=1}^{\infty}b_l\xi_{j,l}^{(1)}(r,\theta).\]于是$(3)$可以作为形函数, 并且$(3)$中前几项的线性组合可以比较准确地逼近$u$.
我们在前面定义$\omega_j$时, $\omega_j$被划分成两个区域:
\[\omega_j=\omega_j^{(1)}\cup\omega_j^{(2)}, \qquad \omega_j^{(1)}\cap\omega_j^{(2)}=\varnothing.\]$u$的真解在$\omega_j^{(1)}$和$\omega_j^{(2)}$上分别是光滑函数(并且还可能是调和函数), 但在$\omega_j$上不一定光滑, 甚至$u$和它的法向导数在穿过两个区域的边界 $\gamma=\partial\omega_j^{(1)}\cap\partial\omega_j^{(2)}$可能是不连续的.
因此我们要构造空间
\[V_j=V_j^{(p)}=\left\lbrace \begin{aligned} &W_{j,1}^{(p)}, \text{ on }\omega_j^{(1)}, \\ &W_{j,2}^{(p)}, \text{ on }\omega_j^{(2)}, \end{aligned}\right.\]满足存在$\xi_j=(\xi_j^{(1)},\xi_j^{(2)})\in V_j^{(p)}$使得
\[\|u-\xi_j^{(1)}\|_{\mathcal{E}(\omega_j^{(1)})}^2+\|u-\xi_j^{(2)}\|_{\mathcal{E}(\omega_j^{(2)})}^2 \text{ is small}.\]记$\chi_j^{(i)}$表示$\omega_j^{(i)}$上的示性函数. 于是$W_{j,i}^{(p)}=W_j^p\chi_j^{(i)}, i=1,2$(对应地, ${^{\mathcal{H}}}W_{j,i}^{(p)}={^{\mathcal{H}}}W_j^{(p)}\chi_j^{(i)}, i=1,2$).
在$V_j^{(p)}$中, 我们需要分别用$\omega_j^{(1)}$和$\omega_j^{(2)}$上的形函数.
3.3 当真解$u$存在奇点时$V_j$的选取
问题$(1)$的解可能是有奇点的, 这可能因为
- 边界$\partial\Omega$有角点;
- 边界条件发生变化, 比如从Dirichlet条件变成Neumann条件;
- 系数$a(x,y)$不是光滑的, 比如可能是分片常值函数;
- 右端项不光滑;
- 真解有边界层(boundary layer).
我们现在只考虑上述前2点. 假设边界$\partial\Omega$在点$A$处有角点:
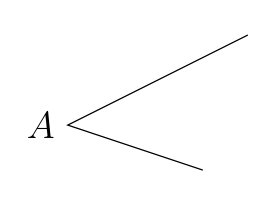
如果问题$(1)$中$f$和$g$充分光滑, 则在$A$的邻域内,
\[u(r,\theta)=\sum_{k=0}^sa_kr^{\lambda_k}\log^{\mu_k}r\psi_j(\theta)+\zeta(r,\theta), \tag{4}\]其中$\lambda_{k+1}\ge\lambda_k$, $\mu_{k+1}\ge\mu_k$, $\psi_j(\theta)$是关于$\theta$的光滑函数, 并且$\zeta(r,\theta)$比求和里面各项都要光滑. 在这里, $(r,\theta)$表示以$A$为原点的极坐标.
注:当$\Gamma_1\cap\Gamma_2=A$时$(4)$式依然成立, 这对应于前面的第2点.
现在我们取$V_j$中的形函数为多项式以及
\[r^{\lambda_k}\log^{\mu_k}r\psi_k(\theta), \quad k=0,1,\cdots,s,\]则用$V_j$中的函数来逼近$u$的误差就是用多项式逼近$\zeta(r,\theta)$的误差.
4 单位分解函数的选取
单位分解函数:Partition of unity(PU) functions.
4.1 单位分解函数的例子
1. 有限元函数
考虑三角剖分的有限元, 取其中一个结点$A_j$. 设区域$\omega_j$是把$A_j$作为顶点的子区域之并. 容易看出, $\lbrace \omega_j\rbrace $可以构成$\Omega$的一个剖分, 即
\[\bigcup_j\omega_j=\Omega.\]然后取$\phi_j$为分片线性函数, 满足
\[\phi_i(A_j)=\left\lbrace \begin{aligned} &1, &&i=j, \\ &0, &&i\ne j. \end{aligned}\right.\]则$\lbrace \phi_j\rbrace $满足一开始在介绍“基本要素”部分的四个条件(2.1)-(2.4), $C_1=1$, $C_2$与区域$\omega_j$的最小角度有关.
2. Shepard函数.
记$B(x,r)$表示以$x$为圆心、$r$为半径的圆盘. 设
\[\Omega=(0,1)\times(0,1),\]以及$A_{\underline{k}}=A_{i,j}=(ih,jh), h=\dfrac{1}{m}, i,j=0,1,\cdots,m$. 设
\[\omega_{\underline{k}}^h=\Omega \cap B(A_{\underline{k}}, Rh),\]其中$R$合适选取使得$\lbrace \omega_{\underline{k}}\rbrace $覆盖$\Omega$. 假设$\phi(r), 0\le r\le\infty$是一阶导数有界的函数, 并且当$0\le r < R$时$\phi(r)>0$; 当$r\ge R$时$\phi(r)=0$. 定义
\[\tilde{\phi}_{\underline{k}}^{(h)}(x,y) =\phi\left(\left(\left(\dfrac{x-ih}{h}\right)^2 +\left(\dfrac{y-jh}{h}\right)^2\right)^{1/2}\right).\]则$\lbrace \tilde{\phi}_{\underline{k}}^{(h)}\rbrace $满足(2.1)(2.3)(2.4)但通常不满足(2.2). 但是我们可以“归一化”. 令
\[\phi_{\underline{k}}^h(x,y) =\dfrac{\tilde{\phi}_{\underline{k}}^h(x,y)} {\sum_{\underline{l}}\tilde{\phi}_{\underline{l}}^h(x,y)},\]则函数族$\lbrace \phi_{\underline{k}}^h\rbrace $满足条件(2.1)-(2.4).
4.2 单位分解函数在构造刚度矩阵上的影响
刚度矩阵的元素包括
\[\int_{\omega_j\cap\omega_l}\nabla\eta_{lk}\cdot\nabla\eta_{ji}\mathrm{d}x. \tag{5}\]计算这些积分需要用数值积分.
(1)我们需要选取合适的$\lbrace \omega_j\rbrace $使得$\lbrace \omega_j\cap\omega_l\rbrace $, $1\le j,l\le N$是简单区域, 以保证数值积分的准确度和计算效率.
例如, 如果$\omega_j$都是圆盘(位于$\mathbb{R}^2$), 则$\omega_j\cap\omega_l$是长得像“镜片”的区域, 在这样的区域上积分比较困难.
再比如, 如果$\omega_j$都是矩形, 则$\omega_j\cap\omega_l$也是矩形, 数值积分比较好计算.
(2)由于$\eta_{ji}=\phi_j\xi_{ji}$, 则在$(5)$中被积函数包含了$\lbrace \phi_j\rbrace $和$\lbrace \nabla\phi_j\rbrace $, 所以$(5)$依赖于单位分解函数$\lbrace \phi_j\rbrace $的光滑性.
4.3 单位分解函数在求解方程$A\boldsymbol{c}=\boldsymbol{f}$上的影响.
$S^{GFEM}$中的形函数可能是线性无关或线性相关的, 它依赖于单位分解函数的选取. 这会导致我们有可能得到奇异或非奇异的线性方程组. 另外, 如果方程组非奇异, 则刚度矩阵的条件数也依赖于单位分解函数的选取.
4.4 误差界
在下面两个式子中:
\[\max\limits_{(x,y)\in\Omega}|\phi_j(x,y)|\le C_1, j=1,\cdots N\]和
\[\max\limits_{(x,y)\in\Omega}|\nabla\phi_j(x,y)|\le\dfrac{C_2}{\mathrm{diam}(\omega_j)}, j=1,\cdots,N\]常数$C_1,C_2$跟$\lbrace \phi_j\rbrace $的选取有关, 进而会影响定理3中的误差估计.
我们不应只是为了一个影响因素来定义单位分解函数. 事实上, 定义$\lbrace \phi_j\rbrace $需要综合广义有限元方法的多个影响因素.
5 小结
用广义有限元方法或者其他类似方法在下面这些问题中能得到比较好的解决:
- 非光滑解的问题(可能因为边界条件或者系数的原因导致的)
- 区域复杂的问题, 生成网格非常困难的情形.
- 边界跟时间有关的问题或者边界开放的问题.
- 某些非线性的问题.
后面我们将作进一步的文献调查.