更新日期:2022年12月21日
Table of Contents
引言
在前一节中, 我们考虑有限元方法的区域是$[0,1]^2$. 目前, 我的目标是求解多尺度有限元方法, 而求多尺度基函数的时候, 需要求一些子区域上的有限元问题. 于是, 如何在不规则的子区域上作网格剖分成为了关键.
三角网格剖分算法是计算几何中的一个分支, 感兴趣的同学可以看参考学习资料中[1]的第25章(Delaunay三角剖分), 或者直接看[2]. 我们不再重复造轮子了, 所以直接采用现成的Python包——CalFEM包.
注: 后来我发现, CalFEM包并不包含加密网格这样的重要功能!!!!于是我只能手动实现, 但是折腾了两天发现还是有一大堆的bug. 于是我又上网找有没有其他FEM包, 最后找到了sfepy包.
但是我们先以CalFEM包为例来演示如何结合自己的程序和现成的网格生成程序来求解PDE.
安装CalFEM
采用
pip install calfem-python
准备工作
我把上一次我们自己写的2D椭圆方程有限元程序优化了一下, 保存为elliptic.py. 主要优化的地方是装配刚度矩阵的时候减少了不必要的循环次数和函数调用. 另外, bdnodes存储的不再是所有边界结点, 而是所有点的边界类型(牺牲空间换时间的一个方法), 不然的话在有些地方可能会出现$O(n^4)$的时间复杂度.
网格生成
我们采用上次的算例. 首先调用一些包, 并使用上次的poimesh函数.
import numpy as np
import Elliptic as fem
import calfem.geometry as cfg
import calfem.mesh as cfm
import calfem.vis_mpl as cfv
import calfem.core as cfc
import calfem.utils as cfu
def poimesh(n): #把[0,1]\times[0,1]分成n^2个单元,采用三角网格
Nb = (n+1)*(n+1) #number of nodes
N = 2*n*n #number of elements
Nlb = 3 #number of nodes on each element
Nbn = Nb #number of boundary nodes
h = 1.0/n
bdnodes = np.zeros(Nbn, dtype=np.int32)
for i in range(n):
bdnodes[i] = 1
bdnodes[n + (n+1)*i] = 1
bdnodes[(n+1) * (i+1)] = 1
bdnodes[n*n+n+i+1] = 1
Tb = np.zeros((N, 3), dtype=np.int32)
for i in range(n):
for j in range(n):
#第ij个单元的结点按顺序是i+(n+1)j, i+1+(n+1)j, i+2+n+(n+1)j, i+1+n+(n+1)j.
Tb[i+j*n*2]=[i+(n+1)*j, i+1+(n+1)*j, i+1+n+(n+1)*j]
Tb[i+j*n*2+n]=[i+2+n+(n+1)*j, i+1+(n+1)*j, i+1+n+(n+1)*j]
#结点与真实坐标的对应关系,存储在information matrix Pb 中
Pb = np.zeros((Nb,2)) #字典
for j in range(n+1):
for i in range(n+1):
Pb[i+j*(n+1)]=np.array([i/n,j/n])
Pb = np.array(Pb)
return Pb, Tb, bdnodes
生成几何图形
下面的代码生成了一个几何图形g, 它包含了四个点$(0,0)$, $(1,0)$, $(1,1)$, $(0,1)$, 以及连接四个点围成的区域.
g = cfg.Geometry() # Create a GeoData object that holds the geometry.
g.point([0, 0])
g.point([1, 0])
g.point([1, 1])
g.point([0, 1])
id_outer = 80 #区域编号
g.spline([0, 1], marker=id_outer)
g.spline([2, 1], marker=id_outer)
g.spline([3, 2], marker=id_outer)
g.spline([0, 3], marker=id_outer)
g.surface([0,1,2,3])
画出几何图形
cfv.figure(fig_size=(5,5))
cfv.draw_geometry(g)
生成网格
mesh = cfm.GmshMesh(g)
mesh.el_type = 2 #Triangle Element
mesh.dofs_per_node = 1 # Degrees of freedom per node.
mesh.el_size_factor = 0.1 # Factor that changes element sizes.
coords, edof, dofs, bdofs, element_markers = mesh.create()
在这里, el_type = 2表示三角单元, dofs_per_node = 1表示每个结点的自由度, 这两个参数在我们这个例子都是固定的. el_size_factor = 0.1表示网格尺寸.
生成网格后, 返回了5个变量, 我们后面要用到这里的coords、edof、bdofs.
edof[:5]
Out: array([[ 72, 81, 102],
[123, 76, 124],
[116, 51, 121],
[104, 52, 122],
[ 52, 104, 123]])
根据输出结果, edof存储的是每个三角单元的三个顶点.
coords[:5]
Out: array([[0. , 0. ],
[1. , 0. ],
[1. , 1. ],
[0. , 1. ],
[0.1, 0. ]])
根据输出结果, coords存储的是结点坐标(按顺序).
bdofs[80][:5]
Out: [1,2,3,4,5]
根据输出结果, bdofs[80]存储的是边界点的编号.
统一记号
我们用Pb和Tb表示结点坐标和单元, 为了统一起见, 我们如下定义:
Pb = coords #nodes
Tb = edof - 1 #Elements
bdnodes = np.zeros(len(Pb), dtype = np.int32) #0: 内部点
for i in bdofs[80]:
bdnodes[i - 1] = 1 #Dirichlet
这里Tb = edof - 1出现了减1, 是因为在CalFEM里面结点是从1开始编号的, 我们要对应于原来的从0开始编号.
画网格
用CalFEM自带的draw_mesh功能可以把网格画出来:
cfv.figure(fig_size=(5, 5))
cfv.draw_mesh(
coords=coords,
edof=edof,
dofs_per_node=mesh.dofs_per_node,
el_type=mesh.el_type,
filled=True,
title="Example 01"
)
我们前面自己写了poimesh函数来生成结点坐标和单元. 事实上也可以利用draw_mesh功能来画网格.
Pb2, Tb2, bdnodes2 = poimesh(10)
cfv.figure(fig_size=(5, 5))
cfv.draw_mesh(
coords=Pb2,
edof=Tb2 + 1,
dofs_per_node=mesh.dofs_per_node,
el_type=mesh.el_type,
filled=True,
title="Example 02"
)

求解PDE
到目前为止, 我们只是用了CalFEM的生成网格功能, 它的解PDE功能我们并不打算使用, 因为我们已经自己实现过一次了.
g = 0
###def c(x):
### return 1
c = 1
###def a(x):
### return 2*(np.pi**2)
a = 2*(np.pi**2)
def f(x):
return 4*(np.pi**2)*np.sin(np.pi* x[0])*np.sin(np.pi* x[1])
u = fem.assempde(Pb,Tb,c,a,f,bdnodes,g)
u2 = fem.assempde(Pb2,Tb2,c,a,f,bdnodes2,g)
画误差图
import matplotlib.pyplot as plt
def plotting(Pb, Tb, u, err = True):
Nb = len(Pb) #Number of nodes
if(err == True):
u_real = np.zeros(Nb)
for i in range(Nb):
u_real[i] = np.sin(np.pi*Pb[i][0])*np.sin(np.pi*Pb[i][1])
E = np.abs(u-u_real) #Error
lower_bound = np.min(E)
upper_bound = np.max(E)
#print(np.min(u),np.max(u))
#print(np.min(u_real),np.max(u_real))
print(np.min(E),np.max(E))
else:
E = u
lower_bound = np.min(E)
upper_bound = np.max(E)
print(np.min(u),np.max(u))
# 更多功能可以参考draw_nodal_values_contourf方法
fig, ax = plt.subplots()
ax.set_aspect('equal')
levels = np.linspace(lower_bound,upper_bound,1000) #对颜色渐进细致程度进行设置
x, y = Pb.T
v = np.asarray(E)
cs = plt.tricontourf(x, y, Tb, v.ravel(), levels)
cbar = fig.colorbar(cs)
plt.show()
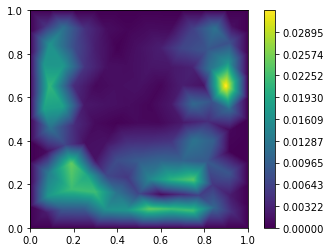
用CalFEM生成的网格解出来的误差:
plotting(Pb, Tb, u, True)
用poimesh网格解出来的误差:
plotting(Pb2, Tb2, u2, True)
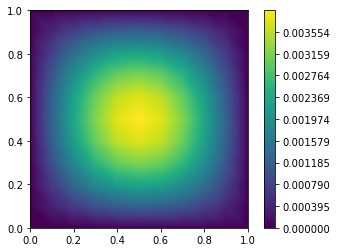
可以发现, 两者之间的最大模误差相差了一个数量级. 但是至于误差阶是不是保持不变, 这里没有办法验证, 在前言我指出我在写加密网格的方法的时候遇到了各种各样的bug, 最主要的bug是边界单元、边界结点之类的处理. 想解决这个方法需要重新修改数据结构, 我们在下篇文章再来解决这个问题.
解复杂区域的问题
你可能会问:误差相差这么多怎么行? 但是它有一个优势是可以解复杂区域的问题. 我们直接贴代码:
生成区域
import numpy as np
import calfem.geometry as cfg
import calfem.mesh as cfm
import calfem.vis_mpl as cfv
import calfem.core as cfc
import calfem.utils as cfu
g = cfg.Geometry() # Create a GeoData object that holds the geometry.
g.point([-1, 0]) #ID: 0
g.point([0,0])
g.point([0,-1])
g.point([1, -1])
g.point([1, 1])
g.point([-1, 1])
g.point([1, 0.25]) #ID: 6
g.point([0.25, 1])
id_outer = 80 #编号
g.spline([0, 1], marker=id_outer) #ID = 0
g.spline([1, 2], marker=id_outer) #ID = 1
g.spline([2, 3], marker=id_outer) #ID = 2
g.spline([3, 6], marker=id_outer) #ID = 3
g.spline([7, 5], marker=id_outer) #ID = 4
g.spline([0, 5], marker=id_outer) #ID = 5
g.circle([6, 4, 7], ID = 8, marker=id_outer) #ID = 8
g.surface([0,1,2,3,8,4,5])
cfv.figure(fig_size=(5,5))
cfv.draw_geometry(g)
生成网格
mesh = cfm.GmshMesh(g)
mesh.el_type = 2
mesh.dofs_per_node = 1 # Degrees of freedom per node.
mesh.el_size_factor = 0.2 # Factor that changes element sizes.
coords, edof, dofs, bdofs, element_markers = mesh.create()
cfv.figure(fig_size=(5, 5))
cfv.draw_mesh(
coords=coords,
edof=edof,
dofs_per_node=mesh.dofs_per_node,
el_type=mesh.el_type,
filled=True,
title="Example 01"
)
求解问题
这里求解的问题是一个不知道真解是什么的问题, $c(x)$是一个分段函数, 定义为
\[c=\left\{\begin{aligned} &0.1, && (x_1-0.5)^2+(x_2+0.5)^2 < 0.09, \\ &0.1, && (x_1+0.5)^2+(x_2-0.5)^2 < 0.09, \\ &1, && \text{其他}, \\ \end{aligned}\right.\]并且边界恒为$0$.
import Elliptic as fem
Pb = coords
Tb = edof - 1
bdnodes = np.zeros(len(Pb), dtype = np.int32) #0: 内部点
for i in bdofs[80]:
bdnodes[i - 1] = 1 #Dirichlet
g = 0
def c(x):
c = 1
if((x[0]-0.5)*(x[0]-0.5) + (x[1]+0.5)*(x[1]+0.5) < 0.09 or (x[0]+0.5)*(x[0]+0.5) + (x[1]-0.5)*(x[1]-0.5) < 0.09):
c = 0.1
return c
a = 0
def f(x):
return 1
u = fem.assempde(Pb,Tb,c,a,f,bdnodes,g)
画图
import matplotlib.pyplot as plt
Nb = len(Pb)
print(np.min(u),np.max(u))
# 更多功能可以参考draw_nodal_values_contourf方法
fig, ax = plt.subplots()
ax.set_aspect('equal')
lower_bound = np.min(u)
upper_bound = np.max(u)
levels = np.linspace(lower_bound,upper_bound,1000) #对颜色渐进细致程度进行设置
x, y = Pb.T
v = np.asarray(u)
cs = plt.tricontourf(x, y, Tb, v.ravel(), levels)
cbar = fig.colorbar(cs)
plt.show()
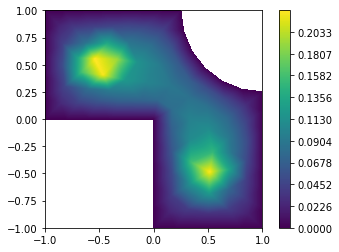
参考学习资料
[1] Jacob E. Goodman, Joseph O’Rourke, Handbook of Discrete Computation Geometry, 2nd Edition, 2004, Chapman & Hall/CRC.
[2] Daniel S.H. Lo, Finite Element Mesh Generation, 2015, CRC.
附录:Elliptic.py
# Elliptic.py
import numpy as np
#from scipy.sparse import csr_matrix
import scipy.sparse as sparse
from scipy.sparse.linalg import spsolve
from scipy import integrate
def gaussquad(p, g, N=7):
#三角形上的Gauss积分, 三角形由p=[p_1,p_2,p_3]围成, 其中p_i都是2维向量.
#g是一个二元函数.
#首先要把函数变换为参考单元上的函数.
def G(x,y): #\hat{x}=(\lambda_1,\lambda_2)\in[0,1]
#x = (\alpha_1-\alpha_0)\lambda_1+(\alpha_2-\alpha_0)\lambda_2+\alpha_0
xx = (p[1][0]-p[0][0])*x + (p[2][0]-p[0][0])*y + p[0][0]
yy = (p[1][1]-p[0][1])*x + (p[2][1]-p[0][1])*y + p[0][1]
return g(np.array([xx,yy]))
val = 0
if(N==1):
val=G(1.0/3,1.0/3)
elif(N==3):
val=(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/3.0
elif(N==4):
val=-9.0*G(1.0/3,1.0/3)/16.0 + 25.0*(G(0.2,0.2)+G(0.2,0.6)+G(0.6,0.2))/48.0
elif(N==7):
val=9.0*G(1.0/3,1.0/3)/20 + 2.0*(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/15.0 + (G(1,0)+G(0,1)+G(0,0))/20.0
val = val * 0.5
return val
def gaussquadnodal(p, f, idx, N=7):
#三角形上的Gauss积分, 三角形由p=[p_1,p_2,p_3]围成, 其中p_i都是2维向量.
#f是一个二元函数.
#计算积分\int_{E_n}f\phi_i dxdy
#idx是计算第几个点的结点基函数. 在参考单元中,第0个点的结点基函数是1-x-y, 第1个点的结点基函数是x, 第2个点的结点基函数y.
#例如idx=1的时候, phi_i变换在参考单元中就会得到\hat{phi}_i=x.
#首先要把函数变换为参考单元上的函数.
def G(x,y): #\hat{x}=(\lambda_1,\lambda_2)\in[0,1]
#x = (\alpha_1-\alpha_0)\lambda_1+(\alpha_2-\alpha_0)\lambda_2+\alpha_0
xx = (p[1][0]-p[0][0])*x + (p[2][0]-p[0][0])*y + p[0][0]
yy = (p[1][1]-p[0][1])*x + (p[2][1]-p[0][1])*y + p[0][1]
v = f(np.array([xx,yy]))
if(idx==0):
v = v * (1-x-y)
elif(idx==1):
v = v * x
elif(idx==2):
v = v * y
return v
#def bounds_y():
# return [0, 1]
#def bounds_x(y):
# return [0, 1-y]
#val = 2*integrate.nquad(G, [bounds_x, bounds_y])[0]
val = 0
if(N==1):
val=G(1.0/3,1.0/3)
elif(N==3):
val=(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/3.0
elif(N==4):
val=-9.0*G(1.0/3,1.0/3)/16.0 + 25.0*(G(0.2,0.2)+G(0.2,0.6)+G(0.6,0.2))/48.0
elif(N==7):
val=9.0*G(1.0/3,1.0/3)/20 + 2.0*(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/15.0 + (G(1,0)+G(0,1)+G(0,0))/20.0
val = val * 0.5
return val
def gaussquadnodalboth(p, a, idx1, idx2, N=7):
#三角形上的Gauss积分, 三角形由p=[p_1,p_2,p_3]围成, 其中p_i都是2维向量.
#f是一个二元函数.
#计算积分\int_{E_n}a\phi_i\phi_j dxdy
#idx是计算第几个点的结点基函数. 在参考单元中,第0个点的结点基函数是1-x-y, 第1个点的结点基函数是x, 第2个点的结点基函数y.
#例如idx=1的时候, phi_i变换在参考单元中就会得到\hat{phi}_i=x.
#首先要把函数变换为参考单元上的函数.
def G(x,y): #\hat{x}=(\lambda_1,\lambda_2)\in[0,1]
#x = (\alpha_1-\alpha_0)\lambda_1+(\alpha_2-\alpha_0)\lambda_2+\alpha_0
xx = (p[1][0]-p[0][0])*x + (p[2][0]-p[0][0])*y + p[0][0]
yy = (p[1][1]-p[0][1])*x + (p[2][1]-p[0][1])*y + p[0][1]
val = a(np.array([xx,yy]))
if(idx1==0):
val = val * (1-x-y)
elif(idx1==1):
val = val * x
elif(idx1==2):
val = val * y
if(idx2==0):
val = val * (1-x-y)
elif(idx2==1):
val = val * x
elif(idx2==2):
val = val * y
return val
val = 0
if(N==1):
val=G(1.0/3,1.0/3)
elif(N==3):
val=(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/3.0
elif(N==4):
val=-9.0*G(1.0/3,1.0/3)/16.0 + 25.0*(G(0.2,0.2)+G(0.2,0.6)+G(0.6,0.2))/48.0
elif(N==7):
val=9.0*G(1.0/3,1.0/3)/20 + 2.0*(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/15.0 + (G(1,0)+G(0,1)+G(0,0))/20.0
val = val * 0.5
return val
def localstiff(p, c):
#拼接局部刚度矩阵\int_{E_n}c\nabla\phi_i\cdot\nabla\phi_j dxdy
S = np.zeros([3,3]) #单刚度矩阵
D = np.array([[-1,-1],[1,0],[0,1]]) #参考单元的梯度
det = (p[1][0]-p[0][0])*(p[2][1]-p[0][1]) - (p[1][1]-p[0][1])*(p[2][0]-p[0][0])
d11 = (p[2][1]-p[0][1]) #d11 = det * \partial\hat{x}_1/\partial x_1
d12 = -(p[2][0]-p[0][0]) #d12 = det *\partial\hat{x}_1/\partial x_2
d21 = -(p[1][1]-p[0][1]) #d21 = det *\partial\hat{x}_2/\partial x_1
d22 = (p[1][0]-p[0][0]) #d22 = det *\partial\hat{x}_2/\partial x_2
#单元的梯度
Nabla = np.zeros([3,2])
for i in [0,1,2]:
Nabla[i] = np.array([D[i][0] * d11 + D[i][1] * d21, D[i][0] * d12 + D[i][1] * d22]) / det
##S[i][j]的计算
if(callable(c)):
for i in [0,1,2]:
for j in [0,1,2]:
def g(x):
return c(x)*(Nabla[i][0]*Nabla[j][0] + Nabla[i][1]*Nabla[j][1])
S[i][j] = gaussquad(p, g) #\int_{E_n}c\nabla_{ni}\cdot\nabla_{nj}dxdy
else:
for i in [0,1,2]:
for j in [0,1,2]:
S[i][j] = (Nabla[i][0]*Nabla[j][0] + Nabla[i][1]*Nabla[j][1]) * c * 0.5
#\int_{E_n}c\nabla_{ni}\cdot\nabla_{nj}dxdy
return S
def assempde(Pb,Tb,c,a,f,bdnodes, g):
"""
输入参数:
Pb: 结点集, 包含结点编号对应的真实坐标
Tb: 单元集, 里面包含每个单元的若干个顶点
c: 函数或标量.
a: 常数
f: 常数或函数
g: Dirichlet边界条件
"""
# assert (neumann_edges == None or h != None) and (neumann_edges != None or h == None), "Neumann边界条件输入不合法"
if(callable(g)==False):
G = g
def g(x):
return G
if(callable(f)==False):
F = f
def f(x):
return F
Nb = len(Pb) #number of nodes
N = len(Tb) #number of elements
Nlb = 3 #number of nodes on each element
Nbn = len(bdnodes) #number of boundary nodes
#Nbe = len(neumann_edges) #number of boundary edges
# 装配稀疏矩阵
A = sparse.lil_matrix((Nb,Nb)) #稀疏矩阵
#\int_{E_n}c\nabla\phi_i\cdot\nabla\phi_j dxdy 我们可以采用Gauss数值积分.
for k in range(N): #第k个单元
p = np.array([Pb[Tb[k][0]], Pb[Tb[k][1]], Pb[Tb[k][2]]])
S = localstiff(p, c) #\int_{E_n}c\nabla\phi_i\cdot\nabla\phi_j dxdy
for i in range(Nlb): #第i个结点
for j in range(Nlb): #第j个结点
r = S[j][i] #单刚度矩阵
A[Tb[k][j],Tb[k][i]] += r
#print(A)
#\int_{E_n}a\phi_i\phi_jdxdy 我们可以采用Gauss数值积分.
if(callable(a)):
for k in range(N): #第k个单元
p = np.array([Pb[Tb[k][0]], Pb[Tb[k][1]], Pb[Tb[k][2]]])
S = np.zeros([3,3]) #单刚度矩阵
##S[i][j]的计算
for i in [0,1,2]:
for j in [0,1,2]: #\int_{E_n}a\phi_i\phi_jdxdy
S[j][i] = gaussquadnodalboth(p, a, j, i)
A[Tb[k][j],Tb[k][i]] += S[j][i]
else:
S = np.array([[2,1,1],
[1,2,1],
[1,1,2] ])/24.0 #单刚度矩阵
for k in range(N): #第k个单元
for i in [0,1,2]:
for j in [0,1,2]:
A[Tb[k][j],Tb[k][i]] += a*S[j][i] #单刚度矩阵
#右端向量
b = np.zeros(Nb)
for k in range(N): #第k个单元
p = np.array([Pb[Tb[k][0]], Pb[Tb[k][1]], Pb[Tb[k][2]]])
for i in range(Nlb): #第i个结点
r = gaussquadnodal(p, f, i)
b[Tb[k][i]] += r
#Dirichlet 边界条件
for i in range(Nbn):
# print(bdnodes[i])
if(bdnodes[i] == 1): #Dirichlet边界
A.data[i] = []
A.rows[i] = []
A[i,i] = 1
b[i] = g(Pb[i])
#Neumann 边界条件
#for j in range(bdedges):
# if(bdedges[k][0] == 2): #Neumann边界
# for i in range(Nlb):
# if(bdnodes[k][0] == 1): #Dirichlet边界
# # Compute r
# j = bdedges[k][1]
# b[i] += 0 #对于一般的情况, 替换为边上的积分
AA = sparse.csc_matrix(A)
u = spsolve(AA, b)
return u