更新日期:2022年12月3日
放出来的代码可以直接运行.
目前关于代码的详细解释还没写完, 尤其是Gauss积分的实现细节.
Table of Contents
引言
所有研究有限元的同学必定会先接触二维椭圆方程, 但是在写代码方面, 此前我只是停留在Matlab的调包当中. 就比如, 考虑问题
\[-\mathrm{div}(\nabla u)=4, \text{ in }\Omega=(0,1)\times(0,1),\]其中边界条件为
\[u|_{\partial\Omega}=0,\]那么用Matlab的PDE ToolBox就是
g=[2,2,2,2; 0,1,1,0; 1,1,0,0; 1,1,0,0; 1,0,0,1; 0,0,0,0; 1,1,1,1]; %区域
n = 8; %网格大小
[p,e,t]=poimesh(g,n);
pdemesh(p,e,t); %画网格
xlim([0 , 1])
ylim([0 , 1])
axis equal;
c=1; a=0; f=4;
b = 'circleb1'; %Dirichlet零边界
u=assempde(b,p,e,t,c,a,f);
pdesurf(p,t,u); %画解
非常的简单. 但是要是想深入了解有限元方法实现, 还是需要自己动手去做. 由于目前的研究需要, 我现在要用Python来实现二维椭圆方程的求解.
问题
求解
\[-\mathrm{div}(c\nabla u)+au=f, \text{ in }\Omega,\]其中边界条件为
\[u|_{\partial\Omega}=g.\]采用三角网格. 它的弱形式为: 求$u\in H^1$使得
\[a(u,v)=(f,v), \qquad \forall v\in H^1(\Omega),\]其中, 双线性形式
\[a(u,v)=\int_{\Omega}(c(x)\nabla u\cdot\nabla v + a(x)uv)\mathrm{d}x.\]基本步骤
设计程序的基本步骤是:
定义结点、边、有限元包含的结点
装配稀疏矩阵
求解稀疏线性方程组
分析数值解、画图等等.
我们先从最简单的三角网格做起. 设区域为$\Omega=(0,1)\times(0,1)$, 把$(0,1)$区间等分成$n$份, 每个小区间长为$h=\dfrac{1}{n}$. 构造网格如下图:
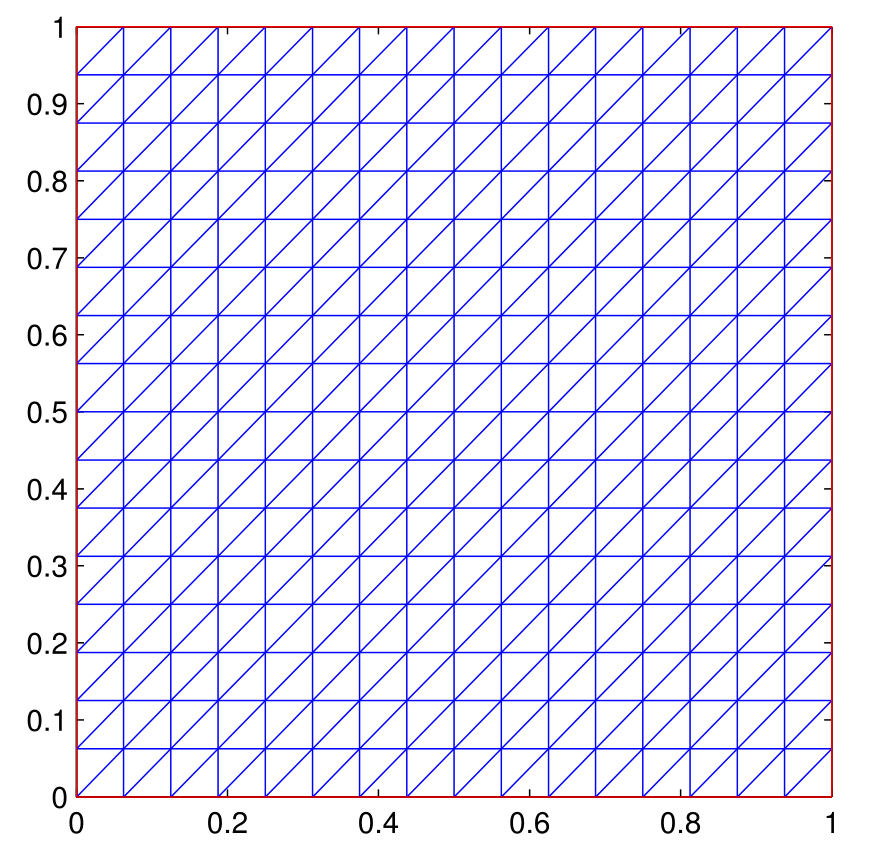
图1:网格($n=16$的情形)
程序实现
网格生成
定义结点
一个网格包含很多结点, 每一行有$n+1$个结点, 我们把结点从下到上、左到右编号.
第0个结点坐标为$(0,0)$的点, 第$n$个结点坐标为$(1,0)$, 第$n+1$个结点坐标为$(h,0)$, $\cdots$, 第$(n+1)^2-1$个结点坐标为$(1,1)$. 如下图.
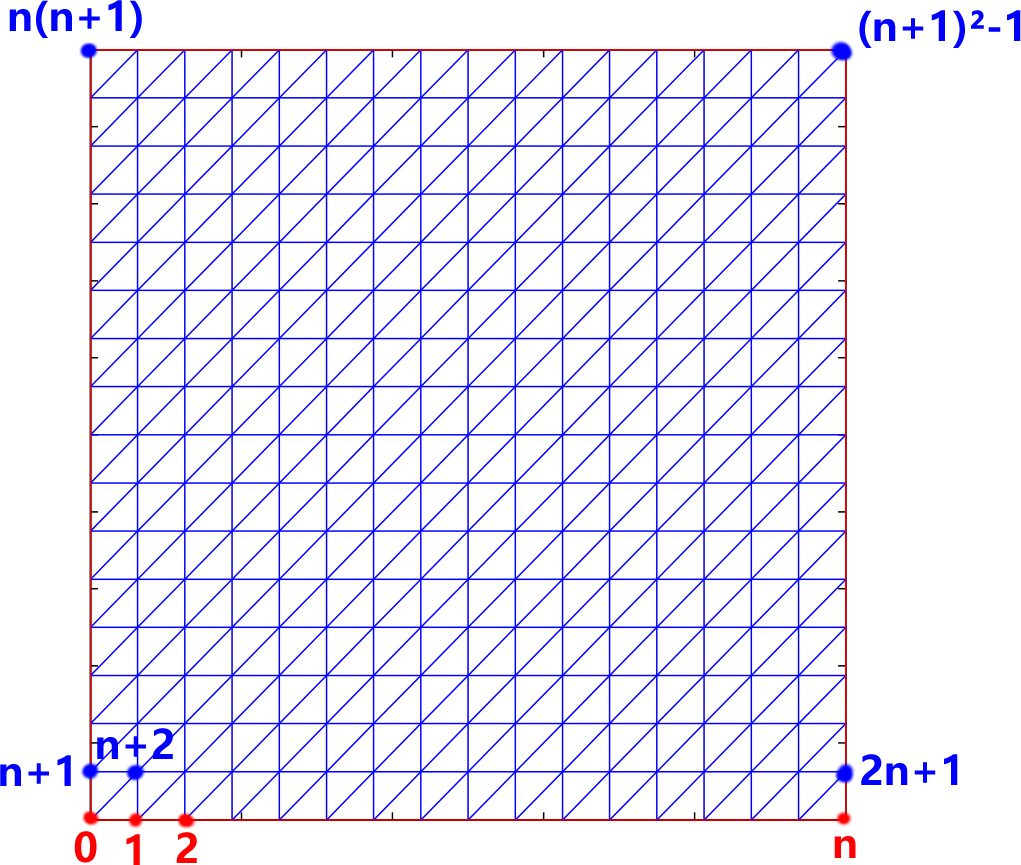
图2:结点编号($n=16$的情形)
我们把结点编号对应的坐标存储在信息矩阵(information matrix) Pb 中.
#结点与真实坐标的对应关系,存储在information matrix Pb 中
Nb = (n+1)*(n+1) #number of nodes
Pb = {} #{}表示一个空的字典
for j in range(n+1):
for i in range(n+1):
Pb[i+j*(n+1)]=np.array([i/n,j/n])
定义边
我们目前还没考虑Neumann边界条件, 暂时先不考虑边的定义(暂时用不上).
定义有限元
每个有限元区域$K$由三个顶点构成, 所以我们只需要存储三个顶点的编号即可.
在第一次写这个部分的时候, 建议把直角对应的顶点放在第一个.
同样, 我们从下到上、从左到右存储, 这里一共有$2n^2$个有限元.
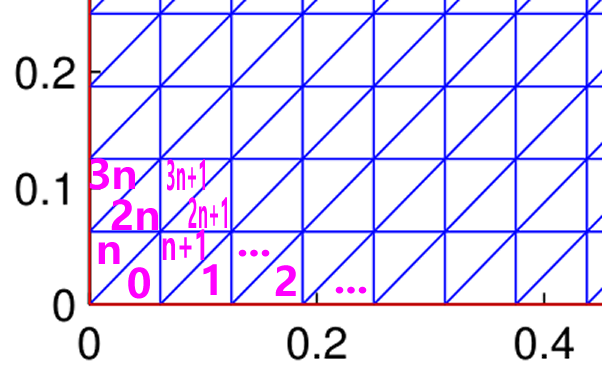
图2:有限元编号(局部)
Nlb = 3 #number of nodes on each element
N = 2*n*n #number of elements
Tb = np.zeros((N, 3), dtype=np.int32)
for i in range(n):
for j in range(n):
#第ij个单元的结点按顺序是i+(n+1)j, i+1+(n+1)j, i+1+n+(n+1)j.
Tb[i+j*n*2]=[i+(n+1)*j, i+1+(n+1)*j, i+1+n+(n+1)*j]
#第ij个单元的结点按顺序是i+2+n+(n+1)j, i+1+(n+1)j, i+1+n+(n+1)j.
Tb[i+j*n*2+n]=[i+2+n+(n+1)*j, i+1+(n+1)*j, i+1+n+(n+1)*j]
定义边界结点
对于边界结点,我们需要指定边界类型和边界点的编号. 边界类型中,用1表示Dirichlet边界条件,2表示Neumann边界条件(后面再用到), 3表示Robin边界条件(后面再用到).
边界结点不用讲究存储顺序.
Nbn = 4*n #number of boundary nodes
bdnodes = np.zeros((Nbn, 2), dtype=np.int32)
for i in range(n):
bdnodes[i][0] = 1 #Dirichlet
bdnodes[i][1] = i
bdnodes[i+n][0] = 1 #Dirichlet
bdnodes[i+n][1] = n + (n+1)*i
bdnodes[i+2*n][0] = 1 #Dirichlet
bdnodes[i+2*n][1] = (n+1) * (i+1)
bdnodes[i+3*n][0] = 1 #Dirichlet
bdnodes[i+3*n][1] = n*n+n+i+1
至此, 关于网格的构造已经完成.
装配矩阵和右端向量
假设$\lbrace \phi_j\rbrace_{i=1}^{Nb}$是线性元空间$V_h$的结点基函数, 满足
\[\phi_i(x_j)=\delta_{ij}, \qquad i,j=1,\cdots,N_b,\]其中$\lbrace x_j\rbrace_{i=1}^{Nb}$是结点. 刚度矩阵$A$是一个$Nb\times Nb$矩阵, 其各个分量为
\[A_{ij}=a(\phi_j,\phi_i)=\sum\limits_{n=1}^{N}\int_{E_n}(c(x)\nabla\phi_j\cdot\nabla\phi_i+a(x)\phi_j\phi_i)\mathrm{d}x.\]这里$E_n$是单元区域. 显然如果$x_i$和$x_j$不相邻, 则$A_{ij}=0$, 所以$A$是个稀疏矩阵. 右端向量$F$的各个分量为
\[F_i=\int_{\Omega}f\phi_i\mathrm{d}x=\sum\limits_{n=1}^N\int_{E_n}f\phi_i\mathrm{d}x.\]计算上述积分需要用到Gauss积分公式. 在计算刚度矩阵$A$的$\int_{E_n}(c(x)\nabla\phi_j\cdot\nabla\phi_i$部分的时候, 我们的步骤如下:
Step 1: 遍历$n=1,\cdots,N$(所有单元), 执行Step 2和Step 3:
Step 2: 计算每个单元$E_n$(由编号为$k_0,k_1,k_2$的结点构成)上的单刚度矩阵$S$. 我们把这个方法的调用记为
localstiff(p,c), 其中$p$是三个结点$k_0,k_1,k_2$, 并且$c$是方程里面的参数.Step 3: 对于$i,j=0,1,2$, 把单刚度矩阵的值$S_{ij}$加在$A$的分量$A_{k_ik_j}$中.
计算$\int_{E_n}a(x)\phi_j\phi_i\mathrm{d}x$和右端向量也是完全类似的, 这里就不写了, 后面我们以代码的形式列出.
由于装配的矩阵是稀疏的, 所以我们要引入稀疏矩阵的包.
import scipy.sparse as sparse
from scipy.sparse.linalg import spsolve
首先用lil_matrix来初始化一个稀疏矩阵, 并初始化右端向量$b$.
A = sparse.lil_matrix((Nb,Nb)) #稀疏矩阵
b = np.zeros(Nb)
关于稀疏矩阵的多种存储方式(不止
lil_matrix)可以在别处搜到.
装配刚度矩阵
如果$c$是一个常数, 那么我们可以很快手动算出单刚度矩阵$S=(s_{ij})$是
\[S=c\begin{pmatrix} 1&-0.5&-0.5 \\ -0.5 & 0.5 & 0 \\ -0.5 & 0 & 0.5 \end{pmatrix},\]其中,
\[s_{ij} = \int_{K}c\nabla\varphi_i\cdot\nabla\varphi_j\mathrm{d}x\mathrm{d}y,\]这里$K$是由$A_0(0,0)$, $A_1(1,0)$, $A_2(0,1)$构成的参考单元. 节点基函数为$\phi_0(x,y)=1-x-y$, $\phi_1(x,y)=x$, $\phi_2(x,y)=y$. 作旋转、平移变换之后得到的结果也是$S$.
这就是为什么我们一开始要求直角对应的结点必须放在第1个位置, 不然的话$S$的某些行和某些列会发生互换. 一般情况下如果想要避免这个错误, 可以直接跳过这部分, 采用“$c$不是常数”的情形来处理, 用的时间可能会长一些.
算完之后把单刚度矩阵拼接成总刚度矩阵即可. (注意下面的Nlb为$3$.)
S = np.array([[1,-0.5,-0.5],
[-0.5,0.5,0],
[-0.5,0,0.5] ]) #单刚度矩阵
for k in range(N): #第k个单元
for i in range(Nlb): #第i个结点
for j in range(Nlb): #第j个结点
r = c*S[j][i] #单刚度矩阵
A[Tb[k][j],Tb[k][i]] += r
如果$c$不是一个常数, 而是一个函数, 那么这就比较复杂了. 此时计算$s_{ij}$需要用到数值积分, 并且单刚度矩阵$S$不尽相同. 我们先用localstiff来表示从给定三个结点构造单刚度矩阵的函数, 后续再补充.
for k in range(N): #第k个单元
p = np.array([Pb[Tb[k][0]], Pb[Tb[k][1]], Pb[Tb[k][2]]])
S = localstiff(p, c)
for i in range(Nlb): #第i个结点
for j in range(Nlb): #第j个结点
r = S[j][i] #单刚度矩阵
A[Tb[k][j],Tb[k][i]] += r
对$au$项的处理也是类似的, 这里略过(后面会附代码).
装配右端向量
右端向量的第$i$个分量就是(其中$E_n$表示第$n$个单元)
\[\int_{\Omega}f\phi_i\mathrm{d}x\mathrm{d}y=\sum\limits_{n=1}^N \int_{E_n}f\phi_i\mathrm{d}x\mathrm{d}y,\]如果$f$是常数, 那么可以算出
\[\int_{E_n}f\phi_i\mathrm{d}x\mathrm{d}y = \dfrac{h^2}{6}f.\] for k in range(N): #第k个单元
for i in range(Nlb): #第i个结点
r = (h**2)*f/6
b[Tb[k][i]] += r
如果$f$不是常数, 那么这时要用到数值积分:
for k in range(N): #第k个单元
p = np.array([Pb[Tb[k][0]], Pb[Tb[k][1]], Pb[Tb[k][2]]])
for i in range(Nlb): #第i个结点
r = gaussquadnodal(p, f, i)
b[Tb[k][i]] += r
关于gaussquad和gaussquadnodal的实现细节, 后面再说.
Dirichlet边界条件
遍历所有边界点bdnodes, 如果一个结点$i$是Dirichlet边界, 那么我们就把其对应的刚度矩阵的第$i$行变成单位向量, 而右端向量的第$i$个分量改为用Dirichlet边界来赋值:
for k in range(Nbn):
if(bdnodes[k][0] == 1): #Dirichlet边界
i = bdnodes[k][1]
A.data[i] = []
A.rows[i] = []
A[i,i] = 1
b[i] = g(Pb[i])
求解
装配完成后, 需要求解线性方程组. 这时我们要用到另外一种稀疏矩阵的存储格式: csc_matrix.
AA = sparse.csc_matrix(A)
u = spsolve(AA, b)
$u$就是我们最终的解向量. 如果想要画出3D的图, 那么点(Pb[i], u[i])就是原来问题在Pb[i]处的数值解.
Gauss积分的数值实现
为了计算如下形式的积分:
\[\int_K\varphi(x)\mathrm{d}x,\]假设$\alpha_i=(a_i,b_i)$是单元$K$的顶点$A_i(i=0,1,2)$的坐标, 定义仿射变换$\hat{x}:=(\lambda_1,\lambda_2)\mapsto x$如下:
\[x=(\alpha_1-\alpha_0)\lambda_1+(\alpha_2-\alpha_0)\lambda_2+\alpha_0.\]这个仿射变换可以把以$(0,0),(1,0),(0,1)$为顶点的参考单元 $\hat{K}$变成以$A_0,A_1,A_2$为顶点的单元$K$.
下面记$\hat{\varphi}(\hat{x})=\varphi(x).$ 显然
\[\int_K\varphi(x)\mathrm{d}x=\dfrac{|K|}{|\hat{K}|}\int_{\hat{K}}\hat{\varphi}(\hat{x})\mathrm{d}\hat{x}.\]$\hat{K}$上的数值积分公式一般形式可以写成
\[\int_{\hat{K}}\hat{\varphi}(\hat{x})\mathrm{d}\hat{x}\sim |\hat{K}|\sum_{n=1}^Mw_n\varphi(Q_n).\]其中$Q_n\in \hat{K}$是积分结点, $w_n$是权重. 如果上式两边对次数小于等于$k$的多项式都相等, 但对$k+1$次多项式不相等, 则称其代数精度是$k$. 下表给出了一些数值积分的例子:
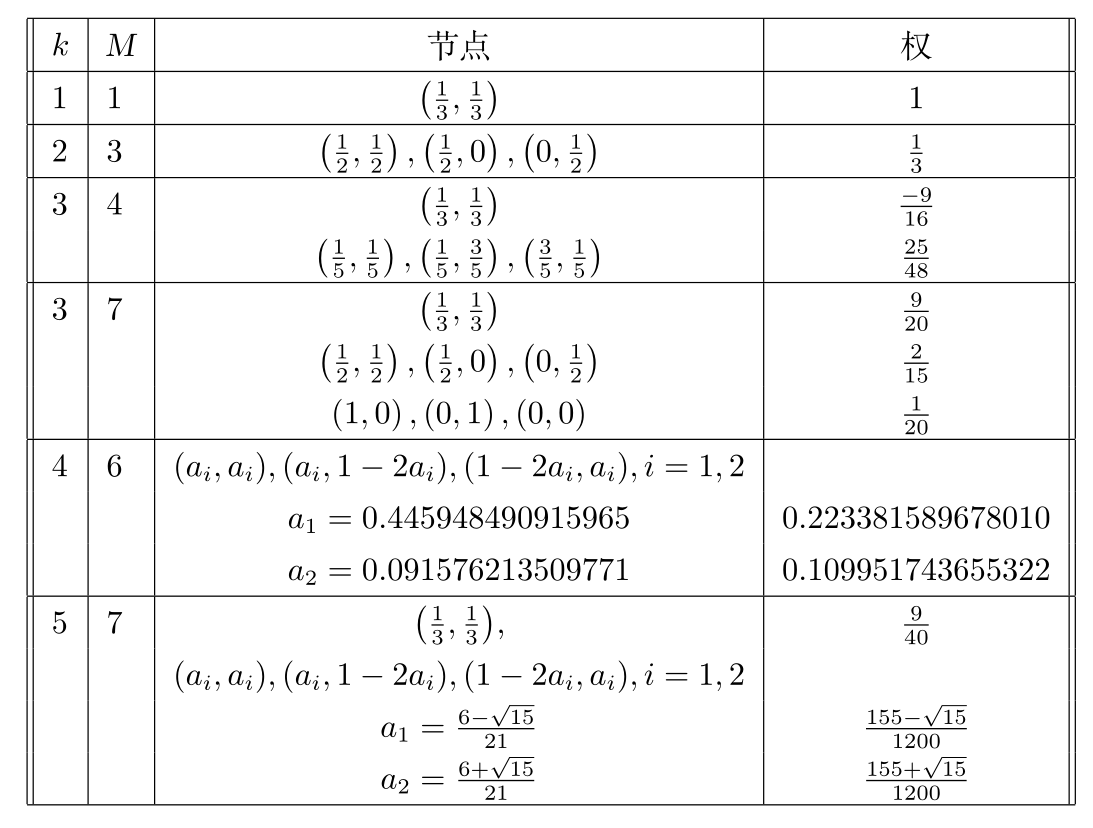
图4:$\hat{K}$上的数值积分公式.
下面的代码具有较高的耦合性(即相同的代码出现多次), 这里为方便起见就不改了.
def gaussquad(p, g, N=7):
#三角形上的Gauss积分, 三角形由p=[p_1,p_2,p_3]围成, 其中p_i都是2维向量.
#g是一个二元函数.
#首先要把函数变换为参考单元上的函数.
def G(x,y): #\hat{x}=(\lambda_1,\lambda_2)\in[0,1]
#x = (\alpha_1-\alpha_0)\lambda_1+(\alpha_2-\alpha_0)\lambda_2+\alpha_0
xx = (p[1][0]-p[0][0])*x + (p[2][0]-p[0][0])*y + p[0][0]
yy = (p[1][1]-p[0][1])*x + (p[2][1]-p[0][1])*y + p[0][1]
return g(np.array([xx,yy]))
val = 0
if(N==1):
val=G(1.0/3,1.0/3)
elif(N==3):
val=(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/3.0
elif(N==4):
val=-9.0*G(1.0/3,1.0/3)/16.0 + 25.0*(G(0.2,0.2)+Grr(0.2,0.6)+G(0.6,0.2))/48.0
elif(N==7):
val=9.0*G(1.0/3,1.0/3)/20 + 2.0*(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/15.0 + (G(1,0)+G(0,1)+G(0,0))/20.0
return val
计算右端向量时需要涉及到$\varphi=f\phi_i$, 此时变换之后的函数为$\hat{\varphi}=\hat{f}\hat{\varphi}_i$, 其中
\[\hat{f}(\hat{x})=f(x), \qquad \hat{\phi}_i=\phi_i,\]由于$\phi_i$是$K$上的结点基函数, 所以$\hat{\phi}_i$是参考单元$\hat{K}$的结点基函数, 于是$A_0(0,0)$, $A_1(1,0)$, $A_2(0,1)$的结点基函数分别为
\[\hat{\phi}_0=1-x-y, \qquad \hat{\phi}_1=x, \qquad \hat{\phi}_2=y.\]所以可以很容易根据$f$的表达式写出$\hat{\varphi}$的表达式(即下面代码中的G(x,y).)
def gaussquadnodal(p, f, idx, N=7):
#计算积分\int_{E_n}f\phi_i dxdy
#三角形上的Gauss积分, 三角形由p=[p_1,p_2,p_3]围成, 其中p_i都是2维向量.
#f是一个二元函数.
#idx是计算第几个点的结点基函数. 在参考单元中,第0个点的结点基函数是1-x-y, 第1个点的结点基函数是x, 第2个点的结点基函数y.
#例如idx=1的时候, phi_i变换在参考单元中就会得到\hat{phi}_i=x.
#首先要把函数变换为参考单元上的函数.
def G(x,y): #\hat{x}=(\lambda_1,\lambda_2)\in[0,1]
#x = (\alpha_1-\alpha_0)\lambda_1+(\alpha_2-\alpha_0)\lambda_2+\alpha_0
xx = (p[1][0]-p[0][0])*x + (p[2][0]-p[0][0])*y + p[0][0]
yy = (p[1][1]-p[0][1])*x + (p[2][1]-p[0][1])*y + p[0][1]
val = f(np.array([xx,yy]))
if(idx==0):
val = val * (1-x-y)
elif(idx==1):
val = val * x
elif(idx==2):
val = val * y
return val
val = 0
if(N==1):
val=G(1.0/3,1.0/3)
elif(N==3):
val=(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/3.0
elif(N==4):
val=-9.0*G(1.0/3,1.0/3)/16.0 + 25.0*(G(0.2,0.2)+Grr(0.2,0.6)+G(0.6,0.2))/48.0
elif(N==7):
val=9.0*G(1.0/3,1.0/3)/20 + 2.0*(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/15.0 + (G(1,0)+G(0,1)+G(0,0))/20.0
return val
下面的代码用来计算
\[\int_{E_n}a\phi_i\phi_j dxdy,\]这跟计算右端向量的时候的处理也是完全类似的.
def gaussquadnodalboth(p, a, idx1, idx2, N=7):
#三角形上的Gauss积分, 三角形由p=[p_1,p_2,p_3]围成, 其中p_i都是2维向量.
#f是一个二元函数.
#计算积分\int_{E_n}a\phi_i\phi_j dxdy
#idx是计算第几个点的结点基函数. 在参考单元中,第0个点的结点基函数是1-x-y, 第1个点的结点基函数是x, 第2个点的结点基函数y.
#例如idx=1的时候, phi_i变换在参考单元中就会得到\hat{phi}_i=x.
#首先要把函数变换为参考单元上的函数.
def G(x,y): #\hat{x}=(\lambda_1,\lambda_2)\in[0,1]
#x = (\alpha_1-\alpha_0)\lambda_1+(\alpha_2-\alpha_0)\lambda_2+\alpha_0
xx = (p[1][0]-p[0][0])*x + (p[2][0]-p[0][0])*y + p[0][0]
yy = (p[1][1]-p[0][1])*x + (p[2][1]-p[0][1])*y + p[0][1]
val = a(np.array([xx,yy]))
if(idx1==0):
val = val * (1-x-y)
elif(idx1==1):
val = val * x
elif(idx1==2):
val = val * y
if(idx2==0):
val = val * (1-x-y)
elif(idx2==1):
val = val * x
elif(idx2==2):
val = val * y
return val
val = 0
if(N==1):
val=G(1.0/3,1.0/3)
elif(N==3):
val=(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/3.0
elif(N==4):
val=-9.0*G(1.0/3,1.0/3)/16.0 + 25.0*(G(0.2,0.2)+Grr(0.2,0.6)+G(0.6,0.2))/48.0
elif(N==7):
val=9.0*G(1.0/3,1.0/3)/20 + 2.0*(G(0.5,0.5)+G(0.5,0)+G(0,0.5))/15.0 + (G(1,0)+G(0,1)+G(0,0))/20.0
return val
拼接单刚度矩阵的数值实现
计算梯度$\nabla\phi_i\cdot\nabla\phi_j$的时候稍微麻烦一些, 同样需要变成参考单元来计算. 由于
\[\phi_i(x)=\hat{\phi}_i(\hat{x}),\]两边对$x_j(j=1,2)$求导, 利用链式法则可得
\[\dfrac{\partial\phi_i(x)}{\partial x_j} = \dfrac{\partial\hat{\phi}_i(\hat{x})}{\partial x_j} = \dfrac{\partial\hat{\phi}_i(\hat{x})}{\partial \hat{x}_1} \dfrac{\partial\hat{x}_1}{\partial x_j} + \dfrac{\partial\hat{\phi}_i(\hat{x})}{\partial \hat{x}_2} \dfrac{\partial\hat{x}_2}{\partial x_j}.\]于是
\[\nabla\phi_i(x) = \nabla\hat{\phi}_i(\hat{x}) J ,\](梯度是行向量. )其中$J$是仿射变换的Jacobi矩阵,
\[J=\begin{pmatrix} \dfrac{\partial\hat{x}_1}{\partial x_1} & \dfrac{\partial\hat{x}_1}{\partial x_2} \\ \dfrac{\partial\hat{x}_2}{\partial x_1} & \dfrac{\partial\hat{x}_2}{\partial x_2} \end{pmatrix}\]$J$的各个分量可以直接计算出来, 用$A_0,A_1,A_2$的坐标表示. 假设
\[B = \det\begin{pmatrix} a_1-a_0 & b_1-b_0 \\ a_2-a_0 & b_2-b_0 \end{pmatrix}\]那么
\[\begin{aligned} &\dfrac{\partial\hat{x}_1}{\partial x_1} = \dfrac{b_2-b_0}{B}, \quad \dfrac{\partial\hat{x}_1}{\partial x_2} = -\dfrac{a_2-a_0}{B}, \\ &\dfrac{\partial\hat{x}_2}{\partial x_1} = -\dfrac{b_1-b_0}{B}, \quad \dfrac{\partial\hat{x}_2}{\partial x_2} = \dfrac{a_1-a_0}{B}. \end{aligned}\]def localstiff(p, c):
#拼接局部刚度矩阵.
D = np.array([[-1,-1],[1,0],[0,1]]) #参考单元的梯度
det = (p[1][0]-p[0][0])*(p[2][1]-p[0][1]) - (p[1][1]-p[0][1])*(p[2][0]-p[0][0])
d11 = (p[2][1]-p[0][1])/det #\partial\hat{x}_1/\partial x_1
d12 = -(p[2][0]-p[0][0])/det #\partial\hat{x}_1/\partial x_2
d21 = -(p[1][1]-p[0][1])/det #\partial\hat{x}_2/\partial x_1
d22 = (p[1][0]-p[0][0])/det #\partial\hat{x}_2/\partial x_2
S = np.zeros([3,3]) #单刚度矩阵
#单元的梯度
Nabla = np.zeros([3,2])
for i in [0,1,2]:
Nabla[i] = np.array([D[i][0] * d11 + D[i][1] * d21, D[i][0] * d12 + D[i][1] * d22])
##S[i][j]的计算
for i in [0,1,2]:
for j in [0,1,2]:
def g(x):
return c(x)*(Nabla[i][0]*Nabla[j][0] + Nabla[i][1]*Nabla[j][1])
S[i][j] = gaussquad(p, g) #\int_{E_n}c\nabla_{ni}\cdot\nabla_{nj}dxdy
return S
def localstiff_a(p, a):
#拼接局部刚度矩阵\int_{E_n}a\phi_i\phi_jdxd.
S = np.zeros([3,3]) #单刚度矩阵
##S[i][j]的计算
for i in [0,1,2]:
for j in [0,1,2]: #\int_{E_n}c\nabla_{ni}\cdot\nabla_{nj}dxdy
S[i][j] = gaussquadnodalboth(p, a, i, j)
return S
算例
考虑问题
\[-\nabla\cdot(\nabla u)+2\pi^2u=4\pi^2\sin(\pi x)\sin(\pi y), (x,y)\in\Omega=[0,1]\times[0,1],\]其中边界条件为
\[u|_{\partial\Omega}=0, (x,y)\in\partial\Omega.\]这个问题的真解是
\[u(x,y)=\sin(\pi x)\sin(\pi y),\]我们取$n=64$, 运行上面的代码得到的数值解记为$u_h$, 真解为$u$, 那么误差的绝对值$e_h=\vert u_h-u\vert $的图像如下:

图5:算例的误差
附录:本节的所有代码
gaussquad、localstiff、gaussquadnodal方法在前面已给出, 这里略.
装配矩阵并求解
import numpy as np
#from scipy.sparse import csr_matrix
import scipy.sparse as sparse
from scipy.sparse.linalg import spsolve
def assempde(Pb,Tb,c,a,f,bdnodes, g):
"""
输入参数:
Pb: 结点集, 包含结点编号对应的真实坐标
Tb: 单元集, 里面包含每个单元的若干个顶点
c: 函数或标量.
a: 常数(暂时没用)
f: 常数或函数
g: Dirichlet边界条件
"""
if(callable(g)==False):
G = g
def g(x):
return G
Nb = len(Pb) #number of nodes
N = len(Tb) #number of elements
Nlb = 3 #number of nodes on each element
Nbn = len(bdnodes) #number of boundary nodes
#Nbe = len(neumann_edges) #number of boundary edges
# 装配稀疏矩阵
A = sparse.lil_matrix((Nb,Nb)) #稀疏矩阵
if(callable(c)==False): #c是常数,那就直接算单刚度矩阵.
S = np.array([[1,-0.5,-0.5],
[-0.5,0.5,0],
[-0.5,0,0.5] ]) #单刚度矩阵
for k in range(N): #第k个单元
for i in range(Nlb): #第i个结点
for j in range(Nlb): #第j个结点
r = c*S[j][i] #单刚度矩阵
A[Tb[k][j],Tb[k][i]] += r
else: #c是个函数, 此时需要算数值积分, 比较麻烦.
#我们可以采用Gauss数值积分.
for k in range(N): #第k个单元
p = np.array([Pb[Tb[k][0]], Pb[Tb[k][1]], Pb[Tb[k][2]]])
S = localstiff(p, c)
for i in range(Nlb): #第i个结点
for j in range(Nlb): #第j个结点
r = S[j][i] #单刚度矩阵
A[Tb[k][j],Tb[k][i]] += r
if(callable(a)==False): #a是常数,那就直接算单刚度矩阵.
S = np.array([[2,1,1],
[1,2,1],
[1,1,2] ])/24.0 #单刚度矩阵
for k in range(N): #第k个单元
for i in range(Nlb): #第i个结点
for j in range(Nlb): #第j个结点
r = a*S[j][i] #单刚度矩阵
A[Tb[k][j],Tb[k][i]] += r
else: #a是个函数, 此时需要算数值积分, 比较麻烦.
#我们可以采用Gauss数值积分.
for k in range(N): #第k个单元
p = np.array([Pb[Tb[k][0]], Pb[Tb[k][1]], Pb[Tb[k][2]]])
S = localstiff_a(p, a) #\int_{E_n}a \phi_i\cdot \phi_j dxdy
for i in range(Nlb): #第i个结点
for j in range(Nlb): #第j个结点
r = S[j][i] #单刚度矩阵
A[Tb[k][j],Tb[k][i]] += r
#右端向量
b = np.zeros(Nb)
if(callable(f)==False): #f是常数,那就直接算.
for k in range(N): #第k个单元
for i in range(Nlb): #第i个结点
r = (h**2)*f/6
b[Tb[k][i]] += r
else: #f是函数
for k in range(N): #第k个单元
p = np.array([Pb[Tb[k][0]], Pb[Tb[k][1]], Pb[Tb[k][2]]])
for i in range(Nlb): #第i个结点
r = gaussquadnodal(p, f, i)
b[Tb[k][i]] += r
#Dirichlet 边界条件
for k in range(Nbn):
if(bdnodes[k][0] == 1): #Dirichlet边界
i = bdnodes[k][1]
A.data[i] = []
A.rows[i] = []
A[i,i] = 1
b[i] = g(Pb[i]) #对于一般的情况, 替换为g(Pb(i))
AA = sparse.csc_matrix(A)
u = spsolve(AA, b)
return u
网格生成
def poimesh(n): #把[0,1]\times[0,1]分成n^2个单元,采用三角网格
Nb = (n+1)*(n+1) #number of nodes
N = 2*n*n #number of elements
Nlb = 3 #number of nodes on each element
Nbn = 4*n #number of boundary nodes
h = 1.0/n
bdnodes = np.zeros((Nbn, 2), dtype=np.int32)
for i in range(n):
bdnodes[i][0] = 1
bdnodes[i][1] = i
bdnodes[i+n][0] = 1
bdnodes[i+n][1] = n + (n+1)*i
bdnodes[i+2*n][0] = 1
bdnodes[i+2*n][1] = (n+1) * (i+1)
bdnodes[i+3*n][0] = 1
bdnodes[i+3*n][1] = n*n+n+i+1
Tb = np.zeros((N, 3), dtype=np.int32)
for i in range(n):
for j in range(n):
#第ij个单元的结点按顺序是i+(n+1)j, i+1+(n+1)j, i+2+n+(n+1)j, i+1+n+(n+1)j.
Tb[i+j*n*2]=[i+(n+1)*j, i+1+(n+1)*j, i+1+n+(n+1)*j]
Tb[i+j*n*2+n]=[i+2+n+(n+1)*j, i+1+(n+1)*j, i+1+n+(n+1)*j]
#结点与真实坐标的对应关系,存储在information matrix Pb 中
Pb = {} #字典
for j in range(n+1):
for i in range(n+1):
Pb[i+j*(n+1)]=np.array([i/n,j/n])
return Pb, Tb, bdnodes
算例
求解PDE
n = 64
Pb, Tb, bdnodes = poimesh(n)
def g(x):
return 0
def c(x):
return 1
def f(x):
return 2*(np.pi**2)*np.sin(np.pi* x[0])*np.sin(np.pi* x[1])
u = assempde(Pb,Tb,c,0,f,bdnodes,g)
画图
import matplotlib.pyplot as plt
X = np.linspace(0,1,n+1)
Y = np.linspace(0,1,n+1)
Z = np.zeros((n+1,n+1))
for i in range(n+1):
for j in range(n+1):
Z[i][j] = u[i*(n+1)+j]
Z_real = np.zeros((n+1,n+1))
for i in range(n+1):
for j in range(n+1):
Z_real[i][j] = np.sin(np.pi*X[i])*np.sin(np.pi*Y[j])
E = np.abs(Z-Z_real)
lower_bound = np.min(E)
upper_bound = np.max(E)
print(lower_bound, upper_bound)
fig, ax = plt.subplots()
levels = np.linspace(lower_bound,upper_bound,1000) #对颜色渐进细致程度进行设置
cs = ax.contourf(X, Y, E, levels,cmap=plt.get_cmap('Spectral'))
cbar = fig.colorbar(cs) #添加colorbar
plt.show()
参考学习资料
[1] 武海军,偏微分方程现代数值方法,上课讲义,2021-2022学期.
[2] 何晓明,有限元基础编程短课(Chapter 3),天元数学东北中心.
链接:https://www.bilibili.com/video/BV1CK411M71t/
font-size:24px (强烈推荐看这个短课学习)