Skip to main content Link Search Menu Expand Document (external link)
Fiddie

完成日期：2022年5月27日

目录

问题

考虑椭圆边值问题$\Delta u=0$, $(x,y)\in\Omega=(-1,1)^2\setminus(-1,0)^2$, 边界条件如下:

\[\left\{\begin{aligned} &u(x,0)=x^4, &&x\in[-1,0], & u(x,y)=1-6x^2+x^4, && y=\pm1, \\ &u(0,y)=y^4, &&y\in[-1,0], & u(x,y)=1-6y^2+y^4, && x=\pm1. \end{aligned}\right.\]

问题1. 证明: 真解关于直线$y=x$对称, 并求真解.

问题2. 使用差分法求方程的近似解, 并与真解比较.

解答

问题1

(1)对称性：只需要证明$u(x,y)=u(y,x)$. 取$v(x,y)=u(y,x)$, 则

\[\left\{\begin{aligned} &v(x,0)=u(0,x)=x^4, &&x\in[-1,0], \\ &v(0,y)=u(y,0)=y^4, &&y\in[-1,0], \\ &v(x,y)=u(y,x)=1-6y^2+y^4, &&x=\pm1, \\ &v(x,y)=u(y,x)=1-6x^2+x^4, &&y=\pm 1. \end{aligned}\right.\]

因此$v$也满足上述椭圆边值问题, 从而$u,v$是同一个椭圆边值问题的解. 取$w=u-v$, 则

\[\Delta w=0\text{ in }\Omega, \qquad w|_{\partial\Omega}=0,\]

由极值原理,

\[\sup\limits_{(x,y)\in\overline{\Omega}}|w(x,y)| =\sup\limits_{(x,y)\in\partial\Omega}|w(x,y)|=0,\]

所以$w\equiv 0$于$\overline{\Omega}$, 从而$u\equiv v$于$\overline{\Omega}$, 即$u(x,y)=u(y,x)$, $\forall (x,y)\in\Omega$. 故$u$关于直线$y=x$对称.

(2)注意到, $\varphi(x,y)=x^4-6x^2y^2+y^4$满足方程和边界条件, 由(1)中证明的方程解的唯一性可知原问题有唯一解

\[u(x,y)=x^4-6x^2y^2+y^4.\]

问题2

Matlab代码

%% Part 1: 用有限差分方法求解L型区域的Laplace方程

n = 80;%必须是偶数
R = 'L';
G = numgrid(R,n+1); %[-1,1]分成n份
% spy(G)  %画G的非零分量图（区域内部点的结点图）
% title('A Finite Difference Grid')

D = delsq(G);%离散Laplace算子
%spy(D) %画矩阵D的非零分量图
%title('The 5-Point Laplacian')

N = sum(G(:)>0);%内部点的个数是N

% 装配右端向量
rhs = zeros(N,1); 
h = 2.0/n; %dx and dy
m = n/2-1; 
for i = 1:m+1
    % x\in[-1,0], y=1
    rhs(1+m*(i-1),1) = rhs(1+m*(i-1),1) + (1-6*(-1+i*h).^2+(-1+i*h).^4); 

    %x\in[-1,0], y=0
    rhs(m*i,1) = rhs(m*i,1) + (-1+i*h).^4;      

    %y\in[-1,0], x=0
    rhs(m*(m+2)+i,1) = rhs(m*(m+2)+i,1) + (-(i-1)*h).^4;   %24   

    %y\in[-1,0], x=1
    rhs(3*m*m+m-1+i,1) = rhs(3*m*m+m-1+i,1) + (1-6*(-(i-1)*h).^2+(-(i-1)*h).^4);   %51   
end
for i = 1:m
    %x=-1, y\in[0,1]
    rhs(i,1) = rhs(i,1) + (1-6*(1-i*h).^2+(1-i*h).^4); 
  
    %x=1, y\in[0,1]
    rhs(3*m*m-1+i,1) = rhs(3*m*m-1+i,1) + (1-6*(1-i*h).^2+(1-i*h).^4);   %47

    %y=-1, x\in[0,1]
    rhs(m*(m+1)+(n-1)*i,1) = rhs(m*(m+1)+(n-1)*i,1) + (1-6*(i*h).^2+(i*h).^4);  

    %y=1, x\in[0,1]
    rhs(m*(m-1)+(n-1)*i,1) = rhs(m*(m-1)+(n-1)*i,1) + (1-6*(i*h).^2+(i*h).^4);  
end

u = D\rhs; % 求解PDE，D是刚度矩阵,rhs是右端向量,u是数值解(排成向量形式)

%%%%%%%%%%%%%%%根据u装配数值解的矩阵
U = G;
%装配U的边界
for xx=1:n+1
    x = -1+(xx-1)*h;
    U(n+2-xx,n+1)=x^4-6*x^2+1;
    y = 1-(xx-1)*h;
    U(1,n+2-xx)=y^4-6*y^2+1;
end

for xx=1:n/2
    y = 1-xx*h;
    U(n+1,n+1-xx)=y^4-6*y^2+1;
    x = (xx-1)*h;
    U(n/2+2-xx,1)=x^4-6*x^2+1;
    x = -1+xx*h;
    U(n+1-xx,n/2+1)=x^4;
    y = -(xx-1)*h;
    U(n/2+1,n/2+2-xx)=y^4;
end

%U的内部按照u来排列
U(G>0) = full(u(G(G>0)));

%画2d彩色图
figure(1)
pcolor(U);
shading interp; 
colorbar; colormap(jet);
xlabel('X');ylabel('Y');
axis square ij

%% Part 2: 画真解 -------------------------------------------
n = 80;
h = 2.0/n;

a = 1:n+1;
b = 1:n+1;
for xx=a
    for yy=b
        x = -1+(xx-1)*h;
        y = -1+(yy-1)*h;
        z(xx,yy)=x^4-6*(x*y)^2+y^4; %真解
    end
end

z(n/2+2:n+1,1:n/2)=0; %左下角区域变成0

figure(2)
pcolor(a,b,z);
shading interp; 
colorbar; colormap(jet);
xlabel('X');ylabel('Y');
axis square ij

%% Part 3: 画误差 -------------------------------------------
figure(3)
pcolor(a,b,abs(z-U));
shading interp; 
colorbar; colormap(jet);
xlabel('X');ylabel('Y');
axis square ij

运行结果

 


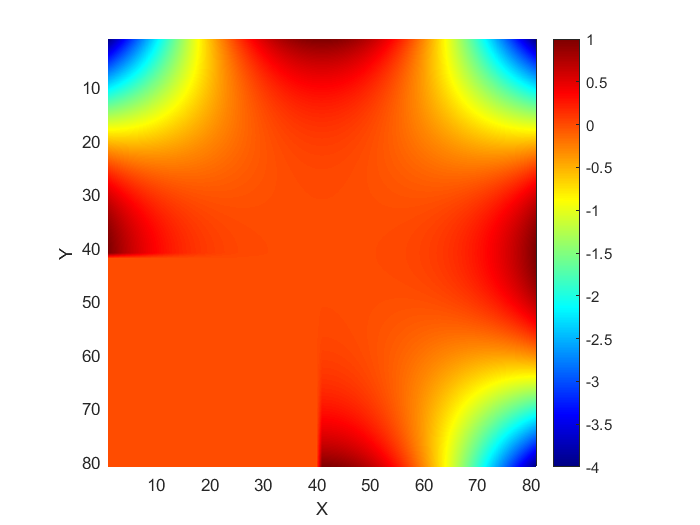
图1：数值解

 


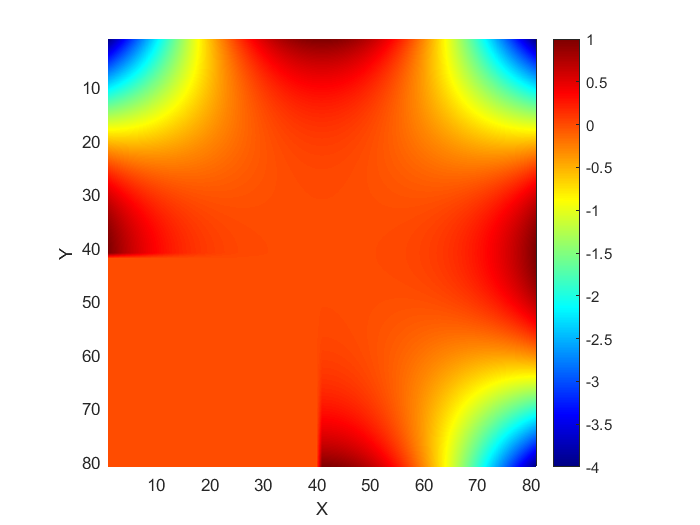
图2：真解

 


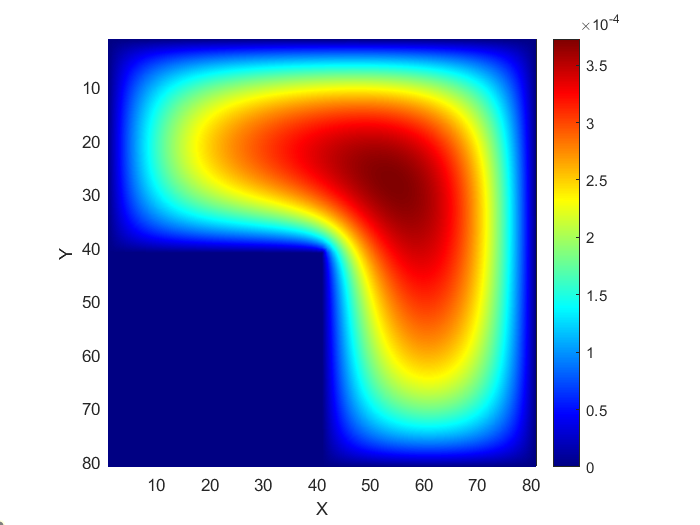
图3：误差