第1周作业

提交截止日期：2024 年 9 月 22 日 23:55:59

HW1

设 $\Omega=(0,1)\times(0,1)$，$\Gamma_ 0:=\lbrace (0,y):0<y<1\rbrace$．给出问题

\[\left\lbrace \begin{aligned} &-\Delta u=f, &&(x,y)\in\Omega, \\ &\dfrac{\partial u}{\partial n}=g, &&(x,y)\in\Gamma_ 0, \\ &u=0,&& (x,y)\in\partial\Omega\setminus\Gamma_ 0 \end{aligned} \right.\]

的离散格式

\[\begin{aligned} &-\Delta_ hu_ {ij}:=-\dfrac{u_ {i-1,j}-2u_ {ij}+u_ {i+1,j}}{h^2} -\dfrac{u_ {i,j-1}-2u_ {ij}+u_ {i,j+1}}{h^2}=f_ {ij}, \\ & \qquad \qquad \qquad 1\le i\le n-1, 1\le j\le n-1. \\ &u_ {ij}=0, \qquad (x_ i,y_ j)\in\partial\Omega\setminus\Gamma_ 0, \\ &\dfrac{4u_ {0,j}-2u_ {1,j}-u_ {0,j-1}-u_ {0,j+1}}{h^2}=f_ {0,j}+\dfrac{2g_ {0,j}}{h}, \qquad 1\le j\le n. \end{aligned}\]

的误差估计．

提示： 最终能证明误差是 $O(h^2)$ 的，仿照讲义上的过程去建立离散极值原理．

易扣分点：构造 $\phi _ {ij} = \dfrac{1}{4}(x_i^2+y_j^2)+x_i$．

最终的误差上界应形如 $Ch^2\Vert u\Vert _ 4$．

HW2

对 Poisson 方程 $-\Delta u=f$，$x\in\Omega$，设 $\mathcal{M} _ {h}$ 为 $\Omega_ h$ 的三角剖分，任意 $K\in\mathcal{M} _ h$，记 $u_ K$ 为 $u$ 在 $K$ 的重心 $C_ K$ 处的近似值，取 $\mathcal{M}_ K$ 为由单元 $K$ 及至少5个邻居单元组成的集合，使得可以由 $\lbrace (C_ {K’},u_ {K’}), K’\in\mathcal{M} _ {h}\rbrace$ 按最小二乘拟合构造一个二次多项式函数，记为 $u_ {h,K}$．定义逼近空间 $U_ h=\lbrace u_ h:u_ h\vert_ K=u_ {h,K}\vert _ K, \forall K\in\mathcal{M}_ h\rbrace$．得 Poisson 方程的单元中心式有限体积离散

\[-\int_ {\partial K}\dfrac{\partial u_ h}{\partial n}\mathrm{d}S=f(C_ K)\vert K\vert.\]

考虑正三角形剖分，对下图中的单元 $K_ 0$，取 $\mathcal{M}_ {K_ 0}=\lbrace K_ 0,K_ 1,\cdots,K_ 6\rbrace$，简记 $u_ i=u_ {K_ i}$，给出 $K_ 0$ 上具体的单元中心式有限体积离散方程．

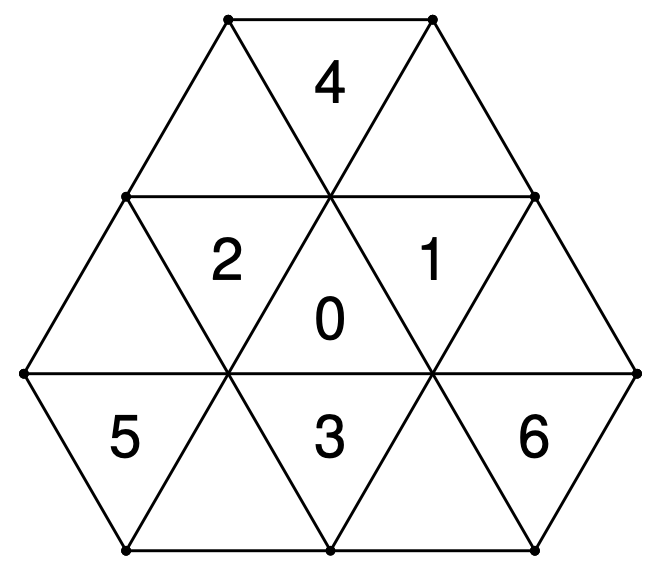
提示： 二次多项式函数形如

\[u_ {h,K}(x,y)=a+bx+cy+dx^2+exy+fy^2,\]

其中 $a,b,c,d,e,f$ 是待定系数．所以有 6 个自由度，需要 6 个方程．

一、$K_ 0$ 是内部单元．

在单元 $K_ 0$ 中，除了重心 $C_ {K_ 0}$ 处的函数值 $u_ 0=u_ {K_ 0}$ 之外，还需要找到至少 5 个邻居单元在重心处的函数值．如果恰好有 5 个单元 $K_ 1,\cdots,K_ 5$，对应重心处的函数值 $u_ 1,\cdots,u_ 5$，那么我们就有 6 个方程

\[u_ {h,K}(C_ {K_ i})=u_ i, \quad i=0,1,2,3,4,5.\]

可以解出 $a,b,c,d,e,f$．

如果有大于 5 个单元 $K_ 1,\cdots,K_ m(m>5)$，对应重心 $C_ {K_ i}$ 处的函数值为 $u_ i(i=1,\cdots,m)$，那么这时需要用最小二乘法来解出 $a,b,c,d,e,f$，即最小化

\[F(a,b,c,d,e,f)=\sum\limits_ {i=0}^m\Big(u_ {h,K}(C_ {K_ i})-u_ i\Big)^2\]

通过 $\nabla F=0$，可以列出 6 个方程，同样可以解出 $a,b,c,d,e,f$．只不过化简 $\nabla F$ 的计算量稍大．

二、$K_ 0$ 是边界单元．

如果单元 $K_ 0$ 是在边界上，可能有下面几种情况：

$K_ 0$ 的一个顶点在边界上；
$K_ 0$ 的一条边在边界上；
$K_ 0$ 的两条边在边界上；
$K_ 0$ 的两个顶点在边界上．

这样可能需要使用边界上的值，而不需要用很多单元重心处的函数值来列方程．

附：计算逆矩阵的相关代码．

syms h C A x0 y0 x1 y1 x2 y2 x3 y3 x4 y4 x5 y5 x6 y6 b;
assume(h,"real")
x0 = 0; y0 = 0;
x1 = h/2; y1 = sqrt(3)*h/6;
x2 = -h/2; y2 = sqrt(3)*h/6;
x3 = 0; y3 = -sqrt(3)*h/3;
x4 = 0; y4 = 2*sqrt(3)*h/3;
x5 = -h; y5 = -sqrt(3)*h/3;
x6 = h; y6 = -sqrt(3)*h/3;
A = [1 x0 y0 x0*x0 x0*y0 y0*y0;
    1 x1 y1 x1*x1 x1*y1 y1*y1;
    1 x2 y2 x2*x2 x2*y2 y2*y2;
    1 x3 y3 x3*x3 x3*y3 y3*y3;
    1 x4 y4 x4*x4 x4*y4 y4*y4;
    1 x5 y5 x5*x5 x5*y5 y5*y5;
    1 x6 y6 x6*x6 x6*y6 y6*y6 ];
C = A'*A;
Cinv = inv(C);
b = [0 0 0 -2 0 -2]; % \Delta u_h 的 Laplacian
D = b*Cinv*A';